![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
上で説明してきたことで、プログラミングの基本は終わりです。もう皆さんは、繰り返しと条件分岐を使って、かなり複雑な処理ができるはずです。そこで、いよいよ実践に移りましょう。
右の図は見たことはありますか?これは、遺伝的浮動のシミュレーションの結果で、集団サイズN=100, 対立遺伝子が2つのとき、片方の対立遺伝子の頻度の変化を表したものです。。最初の世代の対立遺伝子の数は50:50。このグラフを使って、遺伝的浮動とはどういうものか、説明できる人はいますか?また、このグラフはどうやって作ったものですか?
こんな図を作るのはとうてい無理と思っちゃうかもしれません。でも、Rを使ってプログラミングすると、わりと簡単に描けてしまいます。
そこで、ここから先は実践編として、「遺伝的浮動」のシミュレーションをやることにしました。このテーマを選んだ理由は、「生物学科の皆さんになじみが深い」、「Rをつかってやってみて見た目が面白い」、「思ったよりはプログラミングが簡単」というこです。さらに、私にとっては初めて自分で挑戦したシミュレーションで、できあがったグラフを見たときにはかなり嬉しかったものです。
なお、シミュレーション(simulation, 「シュミレーションでは無いですよ!」)は、数学モデルなどを用いて現実に似た状況をコンピュータ上で再現することです。模擬実験とも呼ばれています。(大量の計算を必要とするので、Rのようなインタプリタ型のソフトでは、大規模なシミュレーションは難しいです)
これからシミュレーションを行うのですが、つぎのような状況を想定してみましょう。
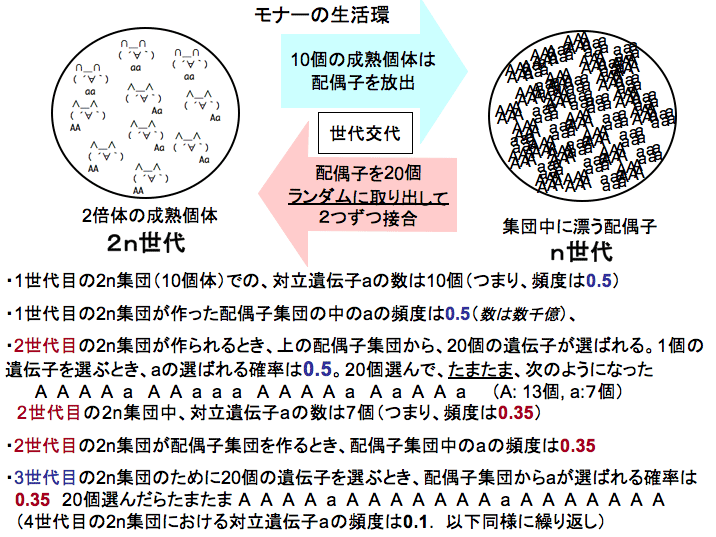
まず、対象とする架空の生物(仮に、「モナー」と呼びます(注:モナーについて詳しく知りたい人は、ウィキペディアで「モナー」を検索してみてください。))は2倍体の生物で、雌雄の区別が無く、繁殖期になると集団内の個体が一斉に配偶子を数千億個ずつ放出して死亡します。配偶子は生息域の空間内をランダムに漂った後、24時間後に、最も近くにある配偶子と接合し、新しい繁殖個体になります。集団の生息域は空間的に限られているため、親世代と同数の子供個体しか、成熟個体になれません。どの子供が成熟個体になるかは、ランダムに決まるものとします。つまり、このモデルだと、世代間で集団サイズに変動は無いということです。モナーにはトンガリ耳と丸耳の2タイプが1対立遺伝子(A, a)で決まることが知られています。トンガリ耳の遺伝子型は(AA, Aa)、丸耳の遺伝子型は(aa)です。
なお、上のモナーの説明は、私が今回のシミュレーションのために、適当に設定したものです。だって、「任意交配をする有限サイズの生物集団から遺伝子をランダム抽出して、同サイズの次世代集団を作った」なんて言い方をするよりは、生物を扱ってる感じがするでしょ?
モナー10個体からなる、1つの集団を考えてみましょう。いまこの集団で、対立遺伝子Aの頻度が0.5, 対立遺伝子aの頻度が0.5のとき(10個体だから遺伝子の総数は、20個です。そのうち半分の10個がAで、10個がaです)。集団中の配偶子の接合はランダムに起こると仮定して、100世代の間に、集団中の対立遺伝子の頻度はどのように変化するでしょうか?
今から実験をするのですから、前もって予想しておいた方が面白そうです この集団の遺伝子頻度が1か0に固定するまでに、何世代ぐらいかかると思いますか? 0-25 26-50 51-75 76-100 100<
それでは、次のプログラムを走らせて、20個の遺伝子中対立遺伝子aが10個ある任意交配集団の、100世代の間のaの遺伝子頻度の変化をみてみましょう。
numa=10 #対立遺伝子aの集団中の個数
for(i in 1:100){ #この行から対応する}までの間を 100世代分繰り返す
counta=0 #次世代にランダムに残るaの値を入れる変数を初期化
for(j in 1:20){ #数千億からなる配偶子プールから1個の配偶子を取り出す試行を20回行う
if ( runif(1) < numa/20 ){ #乱数を一つ発生させ、それが対立遺伝子aの頻度(a/20)よりも小さければ
counta=counta+1 #aの個数を入れるcountaという変数の値を1つ増やす
}
}
out=c(i, counta/20) #何世代目かを表す数字(i)と対立遺伝子aの頻度(a/20)をoutというオブジェクトに入れる
print(out) #outの内容を画面に表示する
numa=counta # aの値を新しい世代の対立遺伝子aの個数(counta)で置き換える
}
繰り返し 代入 条件分岐だけからできていますね。目新しいものと言えば、
runif() 乱数を一つ発生させる。runif(1)とした場合、0から1までの間の値だけです。では、作成過程を1つずつ、順を追って説明します。
20個の遺伝子からなる集団 0世代目の対立遺伝子aの数が10(つまり対立遺伝子aの頻度は0.5) この集団を100世代観察するという条件にしておく
*自分で考えた変数名と定数
numa=10 #0世代目の対立遺伝子aの数。2世代目以降は、シミュレーション実験で抽出されたaの数が代入される
counta=0 #配偶子プールから、次世代の集団に取り出された対立遺伝子aの数。1世代が終わったあとで、
数字が入るので、とりあえず今は0を入れておく
20 #集団の大きさ(つまり、集団に含まれる遺伝子の数)
100 #繰り返しの世代数

*自分で考えたプログラムの構造。コマンドを使って書かなくても、 とりあえず、構造が理解できるように書いてあればよい。

*100回繰り返す繰り返し文の構造
for(i in 0:100) {
<※ここに繰り返される内容が入る>
}※集団中の遺伝子数分、つまり、20回繰り返す文
for(j in 0:20) {
<※※ここに繰り返される内容が入る>
} ※※の操作:
「配偶子を一つ取り出すとき、遺伝子頻度の確率で、対立遺伝子aをひく。もし、対立遺伝子aを引いたら、
aの数を入れておく変数(counta)の値を1つ増やす」
= 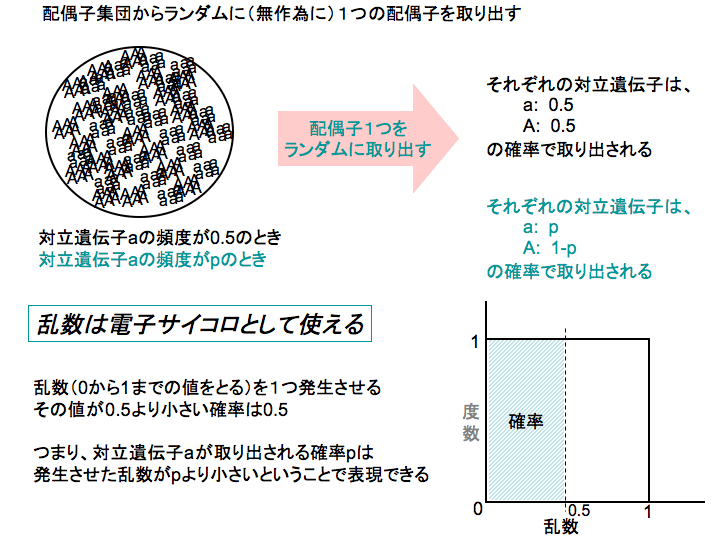

上の『対立遺伝子aを引いたら』(このことは対立遺伝子頻度aの確率で生じる)というのは、
『乱数を一つ発生させたとき、それが対立遺伝子頻度aより低かったら』(これも対立遺伝子頻度aの確率で生じる)と
同じことと考える。そこで、
「乱数を一つ発生させたとき、それが対立遺伝子頻度aより低かったら、
aの数を入れておく変数(counta)の値を1つ増やす」
・内側のfor文の繰り返しが1回終わったら numa = counta counta = 0