![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[worried]](image/face/worried.png) †
†![[smile]](image/face/smile.png) †
†「ユーザー定義関数」なんていうと難しそうだが、ようするに、先ほどまでに作ったプログラムに名前をつけて、いろいろと数値を変えて解析できるようにしようというものだ。こういうときに関数を定義する関数、function()を使う。 例えば、円の面積を計算する関数を作るなら、
menseki=function(r){r*r*pi}
とすれば良い。これで自分独自の関数menseki()ができた。 では、実行してみよう。
menseki(10) #好きな数字を入れて円の面積を計算
演習:1から入力した数値までの全てを横一列に表示させるプログラムを作りdisplayという名前の関数として定義する
display=function(a){ #関数定義の始まり
kekka=c() #kekkaに空ベクトルを代入して初期化
for(i in 1:a){ #a回(iの値を1からaまで変化させる間)繰り返し
kekka=c(kekka,i) #kekkaというベクトルにiを要素として代入
}
print(kekka) #kekkaの内容を表示
} #関数定義の終わり
display(10)
↑を使って何回も実行してみると、結果がいろいろ変わるのがわかる。
演習上の関数の定義方法に従って、入力した数までの合計値を計算するsumupという名前の関数を作成する。下の囲みの中の_の部分(1文字に対応するとは限らない)を埋めて、プログラムを完成しなさい。
sumup = ______ #関数sumpuを定義
kotae = _ #kotaeを初期化
_ (i in ___){ #1からaまで繰り返し
kotae = _____ #kotaeにiの値を足したものとkotaeに代入
} #繰り返し終了
_____ #kotaeを表示
} #関数定義の終了
次のそれぞれのプログラムの_部分に何を入れるべきかを選択肢から選びなさい。また、Rを使って実行してみましょう。
for(i in 1:__){ #{と}の間を10回繰り返す。i の値は毎回1ずつ増える
print(i)
}
選択肢: a) 1 b) 5 c) 10
goukei=0 #goukeiという変数に初期値0を代入
for(i in 1:10) {
goukei=_____+i #goukeiに前回までのgoukeiの値にiの値を足したもの代入
}
print(goukei)
選択肢: a) i b) goukei c) print
goukei=0 #goukeiという変数に初期値0を代入
for(i in 1:10) {
if(i %% 2 __ 0) { # %% は割り算をした余りを返す演算子。3 %% 2 の計算結果は 1 になる
goukei=goukei+i # if文の内容は: 「もし i を 2 で割った余りが 0 ならば、{}内を実行
} #それ以外は何もしない
} #for 文のカッコ閉じるに注意
print(goukei)
選択肢: a) = b) == c) <=
| 演算子 | 意味 | 使用例 |
| + | 足し算 | > 4+3 [1] 7 |
| - | 引き算 | > 4-3 [1] 1 |
| * | 掛け算 | > 4*3 [1] 12 |
| / | 割り算 | > 4/3 [1] 1.333333 |
| ^ | 累乗 | > 4^3 [1] 64 |
| %/% | 整数商 | > 7%/%3 [1] 2 |
| %% | 剰余 | > 7%%3 [1] 1 |
> LETTERS [1] "A" "B" "C" "D" "E" "F" "G" "H" "I" "J" "K" "L" "M" "N" "O" "P" "Q" "R" "S" "T" "U" [22] "V" "W" "X" "Y" "Z" > letters [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t" "u" [22] "v" "w" "x" "y" "z" > month.abb [1] "Jan" "Feb" "Mar" "Apr" "May" "Jun" "Jul" "Aug" "Sep" "Oct" "Nov" "Dec" > month.name [1] "January" "February" "March" "April" "May" "June" "July" [8] "August" "September" "October" "November" "December" > pi [1] 3.141593
| Rの関数 | 意味 | 使用例 |
| c() | ベクトルの作成 | x = c(1, 2, 3, 4) |
| mean() | ベクトルの平均 | mean(1, 2, 3, 4, 5) |
| scan() | コピー・ペーストや手入力でデータをベクトルとして読み込む。 | x=scan() |
| hist() | ヒストグラムを表示 | x=c(1,1, 3, 1, 5, 3, 4, 4); hist(x) |
| summary() | 要約統計量の表示 | x=c(1,1, 3, 1, 5, 3, 4, 4); summary(x) |
| plot() | 散布図の表示 | x=c(1,1, 3, 1, 5, 3, 4, 4); plot(x) |
| print() | オブジェクトを表示 | x=c(1,1, 3, 1, 5, 3, 4, 4); print(x) |
| for(ループ変数 in リスト) {式} | ループ変数をリストの内容に従って、1つずつ変化させる。変化の1回ごとに、{ }の式を実行。 | for(i in 1:10) { print(i) } #注:1:10は 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 を表す |
| matrix(ベクトル, 行数, 列数) | ベクトルを行列に変換して表示 | matrix(1:6, nrow=2, ncol=3) |
| if (条件式) {式1} else {式2} | 条件式が真の時は 式1を実行、偽のときは式2を実行 | if (runif(1) < 0.5) { print("0.5より小さい")} else { print("0.5以上")} |
| runif() | 0-1の乱数を指定した個数発生 | runif(5) |
| function(引数1, 引数2,....){式 } | 自分で関数を定義する | menseki=function(r){r*r*pi} |
| plot.new() | 図を新しく書き直すという関数 |
![[smile]](image/face/smile.png) †
†これまでに学んだ繰り返し・代入・条件分岐の3つの命令それぞれは単純だが、組み合わせれば、かなり複雑なこと表現できる。そこで、今回は、これらの命令を組み合わせて、Rを用いたシミュレーションに挑戦してみよう。
シミュレーションという言葉は「株式シミュレーション」とか「シミュレーションゲーム」とかで聞いたことがあるだろう。日本語にすると、「模擬実験」で、自分では実行が難しい繰り返し実験を、コンピュータに計算させることで行うものだ。コンピュータは単純な繰り返し計算は得意なので、砂粒をばらまいて、ある図形の中に入った数を数えるなんていう作業を、10万回でも、100万回でも繰り返すことができる。
&ref(): File not found: "#10_1.jpg" at page "授業/H21/情報処理/11";
左に1辺の長さが1の正方形と、それに内接する扇形がある。このとき、
正方形の面積は 1 扇形の面積は π/4
この図形の上に、砂粒をばらまいてみる。 砂粒が図形の上にランダムに散らばるとすると、砂粒をすごく沢山まいて数を数えれば、
正方形の中の砂粒の数(n) : 扇形の中砂粒の数(m) = 正方形の面積 :扇形の面積 = 1 : π/4
になると考えられる。つまり
n : m = 1 : π/4 だから、 π = 4m/n
もしあなたが、砂粒をたくさんランダムにまいて、正方形の中の砂粒と扇形の中の砂粒の数を数えることができれば、πの値がわかるということになる。
さて、砂粒を沢山まいて、それが円の中か外かを判定する実験を、コンピュータにやらせるにはどうすればよいだろうか。
まず、点(砂粒)を大量に発生させる必要がある。さて、どうすればいいだろうか?
もうお分かりのように、「繰り返し」命令(for文)を使う。
#とりあえず、1,000つぶの砂をまくことをfor文で表現する
for (i in 1:1000){
<砂を1粒図形の上にまく>
}
次に、砂を1粒図形の上にまいて、それが扇形の中か外かを判定することを考える。
砂を1粒まくことは、無作為に(ランダムに)図形の上に点を打つことと同じことだ。「ランダム」というと、我々はすでに乱数を発生させる方法をしっている。図形の上に1つの点を打つということは、2つの乱数を発生させることで表現できるだろう。
&ref(): File not found: "#10_2.jpg" at page "授業/H21/情報処理/11";
例えば、0-1の範囲の乱数を2つ発生させたら、 (0.230 , 0.782) という2つの数字が得られたとする。この2つの数字が座標上の点を表していると考えると、上の図のようになる。
原点からこの点までの距離が1より小さいとき、この点は扇形の中に入っているということができる。この例では、
0.230^2+0.782^2 < 1
なので、ランダムに発生させた(図形の上に偶然落ちた)1つの点は、扇形の中だったということになる。
point=runif(2) #この命令で、0-1の範囲の乱数を2つ発生させ、pointというベクトルに入れる
このとき、pointに入ったそれぞれの値を指定するには、
point[1] point[2]
のようにカギ括弧[]を使う。
例: プロンプト以降を入力してみよう
> x=c(0.230 , 0.782)
> x[1]
> x[2]
砂粒(点)が扇形の中かどうかを判断するにはどうすれば良いか?これは条件分岐で表現できる。つまり、runif(2)で発生させた2つの数値のそれぞれを2乗して足しあわせたものの平方根が1より小さいか否かを判断する。
#扇形の中かどうかを判断する条件文
distant=sqrt(point[1]^2+point[2]^2) #発生させた2つの乱数の2乗の和の平方根
if(distant<1){ #原点からの距離が1より小さければ扇形の中
<個数を数える>
}
では、個数を数えるにはどうすればよいか?ここでは代入文を使う
#個数を数える部分
kaisu=0 #回数の初期値を0にする
if(distant<1){ #原点からの距離が1より小さければ扇形の中
kaisu = kaisu + 1 #条件にあったとき、kaisuの値を1増やす
}
以上のように、これまでに学習した、繰り返し、条件分岐、代入で、図形の上に砂粒を1000個まく実験が表現できた。πの値は砂粒の個数を4倍して、全体の個数で割ったものだから、以上をまとめると次のようになる。
kaisu=0; #個数の初期値を0にする
for (i in 1:1000) {
point=runif(2)
distant=sqrt(point[1]^2+point[2]^2)
if(distant<1){
kaisu=kaisu+1
}
}
answer=4*kaisu/1000
print(answer)
さらに、functionを使って、好きな回数繰り返せる関数を定義してみよう
simpai=function(x){
kaisu=0; #個数の初期値を0にする
for (i in 1:x) {
point=runif(2)
distant=sqrt(point[1]^2+point[2]^2)
if(distant<1){
kaisu=kaisu+1
}
}
answer=4*kaisu/x
print(answer)
}
> simpai(10)
[1] 2.8
> simpai(100)
[1] 3.16
> simpai(1000)
[1] 3.156
> simpai(10000)
[1] 3.1624
> simpai(100000)
[1] 3.15652
> simpai(1000000) #ここから先は時間がかかるので、授業中はやらない方がいい
[1] 3.13994
> simpai(10000000) #ここから先は時間がかかるので、授業中はやらない方がいい
[1] 3.140556
simpai=function(x){
kaisu=0; #回数の初期値を0にする
for (i in 1:x) {
point=runif(2)
par(new=T) #複数のグラフを重ね合わせる
plot(point[1], point[2], ylim=c(0,1), xlim=c(0,1)) #0-1の範囲で乱数の値をプロット
distant=sqrt(point[1]^2+point[2]^2)
if(distant<1){
kaisu=kaisu+1
}
}
answer=4*kaisu/x
print(answer)
}
&ref(): File not found: "simpai100000.jpg" at page "授業/H21/情報処理/11";
10万回の実行結果。
simpai=function(x){
kaisu=0; #個数の初期値を0にする
for (_ in 1:_) {
for (_ in 1:_) {
point=c(___,___)
distant=sqrt(point[1]^2+point[2]^2)
if(distant<1){
kaisu=kaisu+1
}
}
}
answer=4*kaisu/x^2
print(answer)
}
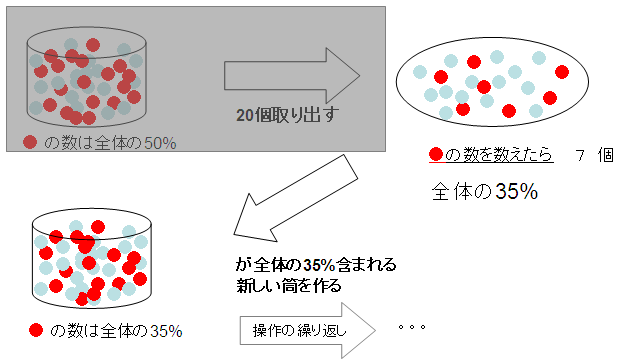
赤玉と青玉が同じ数だけたくさん入った筒から、20個の玉を取り出して、その中に含まれる赤玉の割合に従って筒に含まれる赤玉の個数を変え、また20個取り出す。。。こういう操作を何度も繰り返すというモデルで、何度も実験すると、袋の中の玉の割合がどのように変化するかをシミュレーションで示してみよう。
質問: この実験を何度も繰り返しておこなうとき、 筒の中の玉が赤か白かどちらか1色になってしまうのは、何回目だろうか?
「赤玉と青玉の同じ数入っている筒から無作為に20個の玉を取り出したら、赤玉が7個入っていた」 ----------------------------------------------------- 上でやった操作には、「20個取り出して赤玉かどうか判断する」というところに「繰り返し」が含まれている。 「繰り返し」がはっきりと分かるように説明すると、 1. 筒からボールを一つ取り出す 2. そのボールが赤玉だったら数える(1つ目だったら「一つ」、2つめは「2つ」..)。青玉だったら数えない 3. 1 と 2 の操作を20回繰り返す
この部分を大雑把でいいので、プログラミングしてみる。繰り返しはfor文で表現できる
カウンタの値は最初は0にしておく
for ( 20回繰り返す ) {
if (取り出したのが赤玉だったら) {
カウンタの値を1増やす
}
}
カウンタのところは代入文で表現できる。for文も、Rで実行できる形式に直す
カウンタ = 0
for ( i in 1:20 ) {
if (取り出したのが赤玉だったら) {
カウンタ = カウンタ + 1
}
}
「もし、取り出したのが赤玉だったら」というif文をどうプログラミングすれば良いかが、今回のシミュレーションの最重要ポイントだろう。この部分は乱数を使って表現できる。
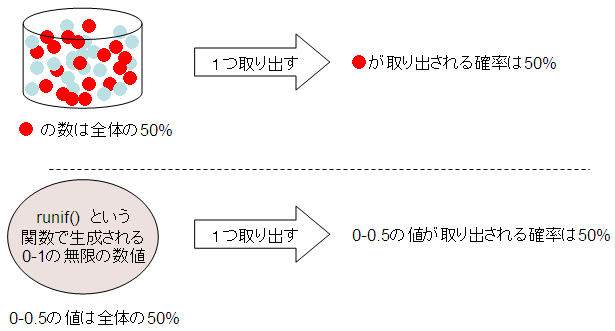
つまり、0-1の範囲の乱数を1つ発生させ、それが0.5よりも小さい値だったら、赤玉が取り出されたとみなせばいい。
乱数を1つ発生させるには runif(1) を使う。
カウンタ = 0
for ( i in 1:20 ) {
if (runif(1) < 0.5 ) {
カウンタ = カウンタ + 1
}
}
print(カウンタ) #この命令で'カウンタ'という変数の内容を表示
これで20個取り出したうちの赤玉の個数を数えるという部分は完成です
上の図で、最初の矢印の部分の操作を行い、筒から取り出した赤玉の数を数えるシミュレーションのプログラミングは終わった。次に、取り出した赤玉の割合になるように筒の中の赤玉の数を変更して、同様の操作を100回繰り返すという部分のプログラミングを考える。繰り返しが含まれているのでfor文を使って大雑把に書くと、
for ( j in 1:100 ) { #さっきiという変数を使ったので、ここではjを使う
※20個取り出して赤玉の数を数える
}
たったこれだけ。上で作った赤玉の数を数えるプログラムを※のところに入れてみると
for ( j in 1:100 ) { #さっきiという変数を使ったので、ここではjを使う
カウンタ = 0
for ( i in 1:20 ) {
if (runif(1) < 0.5 ) {
カウンタ = カウンタ + 1
}
}
print(カウンタ) #この命令で'カウンタ'という変数の内容を表示
}
ん??これでは上の図の例で、20個取り出した中に含まれていた赤玉の数の割合に、筒の中の赤玉の割合を変更したことが反映されていない。取り出した赤玉の数は、内側のfor文が終わった後に、カウンタの値を20で割ることで求められるから、「赤玉の割合」という変数を一つ作って、毎回、新しい値をこの変数に入れるようにしよう。
赤玉の割合=0.5 #初期値は0.5
for ( j in 1:100 ) { #さっきiという変数を使ったので、ここではjを使う
カウンタ = 0
for ( i in 1:20 ) {
if (runif(1) < 赤玉の割合 ) {
カウンタ = カウンタ + 1
}
}
赤玉の割合 = カウンタ/20 #20個の中の赤玉の割合を算出
print(カウンタ) #この命令で'カウンタ'という変数の内容を表示
}
あとは結果をプリントする文を入れれば完成。何回目に1色になったかが分かるように、j の値も一緒にプリントしよう。
赤玉の割合=0.5 #初期値は0.5
for ( j in 1:100 ) { #さっきiという変数を使ったので、ここではjを使う
カウンタ = 0
for ( i in 1:20 ) {
if (runif(1) < 赤玉の割合 ) {
カウンタ = カウンタ + 1
}
}
赤玉の割合 = カウンタ/20 #20個の中の赤玉の割合を算出
結果=c(j, 赤玉の割合)
print(結果)
}
できる人は、結果をグラフに表示してみよう。
実は、今作成したシミュレーションは、生物学科の人は皆知っている遺伝的浮動のシミュレーションだ。この例で、それぞれの変数は次のように対応している。
赤玉の割合: 遺伝子頻度の初期値 繰り返し数(ここでは100回): 世代数 筒の中の玉の数 (ここでは20): 集団サイズ
昨年度までは、最初から遺伝的浮動のシミュレーションを目指して授業を行ったのだが、今年度は話を少し単純にして、筒の中の玉の個数の変化という実験にしてみた。遺伝的浮動に興味がある人は、昨年度の授業ページを参照して欲しい。
一昨年、同様の授業を行ったところ、受講生から次のような質問があった。
「こういうシミュレーションのプログラミングって、これから生物学を学ぶのに、どのくらい必要なんですか?」
これまでプログラミングなどしたことの無い人にとって、とても素朴な疑問だろうと思う。そこで、次のように答えておいた。
画一的な答えは難しいです。シミュレーションそのものが直接必要になるような分野もあれば、そうでない分野もあります。 ただ、私は、プログラミングは、生物学における発展的な情報処理をする上での基本技だと考えています。 千葉大の研究室に限って言えば、プログラミング技術が無いと卒業研究が終わらないというところは 現時点では(たぶん)無いでしょう。但し、プログラミングができると、卒業研究や修士の研究でより 進んだことができたり、理解が深まったり、研究が楽になるようなところはいくつもあります。 将来、数理生物学、理論集団遺伝学、進化生態学、バイオインフォマティクスを志す人には、 敢えて、不可欠な技術だと言っておきます。
./11
*第11回授業・基本課題 **氏名: **課題への回答 -今日の授業の進み方は?(はやい、丁度いい、おそい) --回答: -今日の授業の難しさはどう感じましたか(簡単 丁度いい 難しい): --回答: -難しいと答えた人は、特にどの点が難しかったですか?: --回答: -今日の授業は(分かった 半分ぐらいは分かった 分からなかった): --回答: -分からないと答えた人は、特にどの点が分からなかったですか?: --回答: -今日の講義で分からなかった用語があったら挙げてください: --回答: -授業に関する要望・質問があったらなんでもどうぞ: --回答: -課題2の答え --問1 --【1】: --【2】: --【3】: --【4】: --問2: ---追加する命令と追加する場所: ---得られたヒストグラム: -課題3の答え --問1 --【1】: --【2】: --【3】: --問2-1: --問2-2: --問3:
下のプログラムは、正常なコイン(表、裏の出る確率はそれぞれ0.5)を100回投げて、表の出た回数を記録するという実験を、1000回繰り返すシミュレーションのプログラムです。
omote=0 #表の出る回数を初期化
kekka=c()
for(i in 1:【1】){
for (i in 1:【2】){
if(runif(1)<【3】){
omote=【4】+1
}
}
kekka=c(kekka,omote)
omote=0 #表の出る回数を初期化
}
print(kekka)
下のプログラムは遺伝的浮動をシミュレートするRのプログラムです。このシミュレーションで観察する集団の数(num_repeats)、1集団あたり観察する世代数(num_generations)、集団サイズ(遺伝子数)(size_population)、0世代目における対立遺伝子aの数(num_a_allele)を与えて実行すれば、、ランダムに選ばれる遺伝子が、次世代の集団の遺伝子頻度にどのように影響するかを、シミュレートする集団数(観察集団数)の数だけ色つきの折れ線グラフで表示することができます。下のプログラムを見て以下の問に答えなさい。
drift= function(num_repeats,num_generations,size_population, num_a_allele){
results=c()
a=num_a_allele
for(i in 1:【1】){
for(j in 1:【2】){
count_a=0
for(k in 1:size_population){
if ( runif(1) < a/【3】 ){
count_a=count_a+1
}
}
a=count_a
results=append(results, a/size_population)
}
a=num_a_allele
}
rmatrix=matrix(results, nrow=num_generations, ncol=num_repeats)
return(matplot(rmatrix, type="l"))
}
num_repeats, num_generations, size_population, num_a_allele
1. 実験の繰り返し数10回、1集団での観察世代数500世代、集団サイズ(遺伝子数)200, 初期状態での対立遺伝子aの数100 2. 実験の繰り返し数10回、1集団での観察世代数100世代、集団サイズ(遺伝子数)20, 初期状態での対立遺伝子aの数10 いずれの場合についても、できたグラフをWinShotで切り取って、課題提出ページに貼り付けなさい(注:1番目のシミュ レーションの実行には、数分かかるかもしれません)(注:あまり大きい図(画面全面に広がる図とか)にはしないでく ださい)