![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[worried]](image/face/worried.png) †
†まずは、授業Moodleページから、演習1のグループワークをやってみよう。
千葉大学のSkipwiseプログラムでは、留学をカリキュラムの一環として位置づけ、平成28年までの5年間に学部学生の30%が留学を経験することを目標としている。そこで海外留学について考えてみよう。なお、今年度の短期留学プログラムの説明会が、今週の金曜に行われるので、興味のある人は参加してみよう。
![[smile]](image/face/smile.png) †
†さて、先週は最後の方で簡単にしか説明しなかったR。
今週は、自分で操作して、好きなグラフを描けるところまでやってみよう。今後の研究やレポートでもかならず役に立つので、全員ができるようになることを目指したい。。
数年前から大学の教育用端末に、Rがインスト−ルされているので、授業ではインストール作業は不要になった。
おうちの自分のパソコンでRを使いたい場合、
のいずれかにアクセスして、ダウンロードしてインストールする。Windows , Mac, Linuxのどの環境でも使える。
では、スタートメニューから、Rを起動しよう。
R起動すると~、画面が切り替わり、小さいウィンドウの中にいくつかのメッセージと、一番最後に、
>
が表示される。この">"をプロンプトと言う。プロンプトの右側には通常、カーソルがあり、「このマークの後に何かコマンド(命令)を打ち込んでくださいよ」とあなたに促している。式を入力して、最後にenter(or returnキー)を押せば計算される。
![[smile]](image/face/smile.png) †
†以下、Rを使った簡単な計算。プロンプト(>)から右の部分をコピーペーストすれば、計算できる。
> 4/3*pi*5^3
> pi #円周率が表示される(デフォルトでは小数点以下6桁まで)
> (1+ 2 + 3 + 4 + 5 )/3 #式の間に半角スペースがいくつか入っても大丈夫
【ここでキーボードの上矢印(↑)を押す: 前に入力した命令を表示させることができる】 > (10 + 2 + 3 + 4 + 15 )/3 #前に入力した式が表示されるので、左矢印(←)でカーソルを動かし修正
> 1035 %% 27
> 3^7
>sqrt(27)
| 演算子 | 意味 | 使用例 |
| + | 足し算 | > 4+3 [1] 7 |
| - | 引き算 | > 4-3 [1] 1 |
| * | 掛け算 | > 4*3 [1] 12 |
| / | 割り算 | > 4/3 [1] 1.333333 |
| ^ | 累乗 | > 4^3 [1] 64 |
| %/% | 整数商 | > 7%/%3 [1] 2 |
| %% | 剰余 | > 7%%3 [1] 1 |
Rでは、好きな名前をつけたオブジェクト("もの")に、数値や文字列などのデータを代入できます。オブジェクトには大文字小文字の区別があります。
> x = 3 #xに3という数字を代入した > X = 4 #Xに4という数字を代入した > x + X #xとXの足し算 (なお、#の後はコメント文と呼ばれ、処理には関係の無い説明を書いておける)
なお、上では"="を使って数値を代入しましたが、 "<-"を使っても同じことができます。
> x <- 3 > X <- 4 > x+X
(Rの代入はもともと "<- " だけだったが、比較的最近、 " = " も使えるようになった。この授業では=を使う)
![[smile]](image/face/smile.png) †
†みなさんは、沢山のデータを1まとめにして扱う方法をすでに知っている。 例えばエクセルを使った計算では、
| 10.4 | 5.6 | 3.1 | 6.4 | 21.7 |
という表を使ってデータを一まとめにし、sum()関数をつかったり、1つのセルに5を足すという計算結果を全部のセルにコピペして、全ての値に5ずつ0足した結果を得たりした。
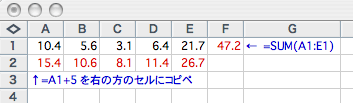
でも、Rのように、命令文を1行ずつ入力して計算するソフトウェアの場合、データをまとめて扱うにはどうすればいいだろうか?
もちろん、下のように1行ずつ計算式を打ち込んでも答えはでるが、データの数が多くなると、面倒すぎる。
(こんなやり方だと面倒くさい) > 10.4+5.6+3.1+6.4+21.7 > 10.4+5 > 5.6+5
そこで、Rでは、たくさんのデータを一まとめにして扱うときには、カンマで区切って横1行に並べて使う。このようなデータの構造をベクトルと呼ぶ。ベクトルとうと、高校の数学でやった「大きさと方向をもった量」を思い出すと思うが、
Rで使うベクトルは、同じ種類のデータに順番をつけて並べたもの
と定義しておこう。これは、Rが沢山のデータをまとめて処理するために用いる、データの構造だ。例えば、
(10.4, 5.6, 3.1, 6.4, 21.7)
というデータの集まりは、同じタイプのデータに順番をつけてひとまとめにしたものであり、Rでいうところのベクトルだ。
そして、Rでデータを一まとめにして使うときに必要なのが、c()という関数。
| Rを使う上で、これだけは絶対に覚えておこう |
| Rでデータを一まとめにして扱うときには、 c( ) という関数を使う |
例えば、上のデータを、x というオブジェクトに代入したいときには、
x=c(10.4, 5.6, 3.1, 6.4, 21.7)
という命令を使う。上の命令を入力した後、「 x 」とだけ入力すると、xの内容が表示される。
> x [1] 10.4 5.6 3.1 6.4 21.7
上の結果に表示された[1]は何だろうか?これは、表示された行の最初の数字が、ベクトルの1番目の要素だということを意味している。では、次のようなベクトルをyに代入して、内容を表示させてみよう。
> y=c(1984,1985,1986,1987,1988,1989,1990,1991,1992,1993, 1994,1995,1996,1997,1998,1999,2000,2001)
ウィンドウの大きさによって表示のされ方は異なるが、もし1行に収まらなければ、
> y [1] 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 [15] 1998 1999 2000 2001
というように、2行目の始まりに[15]というような数字が表示される。これは、2行目が15番目の要素から始まっていることを示している。
「ベクトル」とは、同じタイプのデータに順番をつけて一まとめにしたものだった。では、一まとめの中から、例えば、「5番目の要素」だけを取り出すにはどうすればいいだろうか?勘のいい人はもう気づいているかもしれないが、
> y[5] [1] 1988
と、オブジェクトの名前に順番を[]に入れたものをくっつける事で、目的の要素を取り出すことができる。
では、Rで、沢山のデータを一まとめにして、いろいろ計算してみよう。
まずはおさらい。上で出てきた、 c() という関数を使って、オブジェクトにデータを代入でする。
> x=c(1,2,3,4,5,6,7) >
entterキーを押しても何もおこらない?いえいえ。エラーメッセージが何も表示されず、新しいプロンプトが表示されたら大成功。
(もし、上のようにならなかった人は、半角・全角の文字の違いとコンマやカッコに注意してもう一度やってみよう。)
では、プロンプトの後に"x"と入力して、結果を見てみよう。
>x [1] 1 2 3 4 5 6 7
上の様に表示されれば「xというオブジェクトに(1,2,3,4,5,6,7)が代入されたことになる。では、このデータを対象に、統計解析の基本である平均値の計算を計算してみよう。
mean()という関数(meanは英語で平均値の意味)で一まとめにしたデータ(ベクトル)の平均値が計算できる。 命令の入力に自信の無い人は、下の囲みの中をコピー・ペースト。 >mean(x) [1] 4
平均値"4"が表示されれば大成功(これで、あなたがRを使って行う、初めての統計解析は、無事に成功した)
では、数値をもう少し変えて、自分の好きな値で計算してみよう。。。
上で説明したように、キーボードの"↑"記号を何回か押してみると、
> x=c(1,2,3,4,5,6,7)
と表示された。そしたら"←"と"Back space"などを使って、数値を好きに変更して、最後に"Enter"キーを押そう。
> x=c(1232,223.33,3 ,4 , 5666)
半角文字であるかぎり、別にスペースがいくつ入っていても大丈夫。入力したら、上と同じことをしてみると、
> x [1] 1232.00 223.33 3.00 4.00 5666.00 > mean(x) [1] 1425.666
これで、自分の好きな値を入力して、平均を計算することができた。
![[smile]](image/face/smile.png) †
†では、いよいよ、Rで簡単なグラフを描いてみよう。まずやらなければならないのは、
オブジェクトにデータを代入
データは、前回授業で用いた死亡率の表を使う。扱いやすいように、エクセルファイルにしたものを、ここに添付しておくので、ダウンロードして開いてみよう。
#data1にデータを入力
data1 = read.table("<ファイルへのパス>practice3.csv", header = TRUE, sep=",")
##ファイルへのパスを知るには、ダウンロードしたpractice3.csvを、Rのファイルメニューから
「ソースを開く」で開いてみる。コンソールに、パス(ファイルの場所を示す文字列)が表示される
pairs(data1)
年のデータ data1$year 癌のデータ data1$cancer 年・癌のプロット plot(data1$year,data1$cancer)
まず、年、結核、心疾患のそれぞれの男女別のデータを、それぞれ
年 を year に 結核・男 を m_k 結核・女 を f_k 心疾患・男 を m_h 心疾患・女 を f_h
に代入しよう。
このとき、上でつかったc()という関数を使うのではなく、scan()という関数を使うと、エクセルからのコピーペーストで値をオブジェクトに代入できる。
まず、1986-2006の年のデータをyearに入れるには、
> year = scan() #ここでEnterを押す 1:
すると、「1:」という表示になるので、、エクセルのシートから1986から2006までのデータをペーストすると
1: 1986 2: 1987 3: 1988 4: 1989 5: 1990 6: 1991 7: 1992 8: 1993 9: 1994 10: 1995 11: 1996 12: 1997 13: 1998 14: 1999 15: 2000 16: 2001 17: 2002 18: 2003 19: 2004 20: 2005 21: 2006 22: #最後にEnterを押す
これで21年分の年のデータが、yearに入った。試しに
>year
と入力してみよう。下のようになるはずだ。
[1] 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 [16] 2001 2002 2003 2004 2005 2006
男性の結核のデータをm_kというオブジェクトに入力する場合、 > m_k = scan() 1: #ここで、男性の結核のデータをペースト.
. 22: #最後にEnterを押す
> year [1] 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 [16] 2001 2002 2003 2004 2005 2006 > m_k [1] 3112 2959 2954 2676 2745 2449 2514 2424 2290 2267 2064 1955 1977 2114 1876 [16] 1715 1584 1615 1555 1579 1517 > f_k [1] 1058 1063 918 851 919 876 833 825 804 911 794 787 818 821 780 [16] 776 733 722 775 717 752 > m_h [1] 72072 72566 78640 77901 81774 83646 86384 88309 78868 69718 68977 69776 71134 [14] 73979 72156 72727 74986 77989 77465 83979 82811 > f_h [1] 70509 71343 79280 78930 83704 85232 89162 91988 80711 69488 69252 70398 71986 [14] 77100 74585 75565 77532 81556 82160 89146 90213
それでは最も基本的なグラフ作成関数であるplot()を使ってみよう。操作は、以下のように入力するだけ。
>plot(year,m_k)
下のようなグラフが表示されただろうか?
&ref(): File not found: "#6_2.gif" at page "授業/H26/情報処理/07";
折れ線グラフにしたければ、こうやってみるといい。
> plot(year,m_k, type="l")
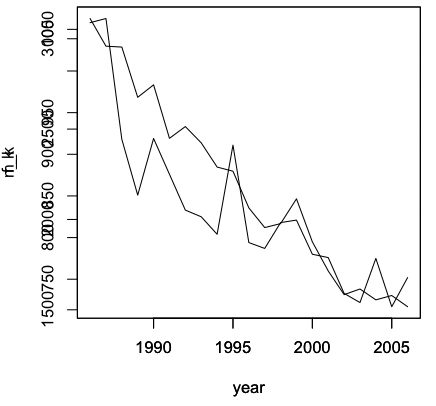
それでは、男女の結核による死亡者数の推移を、1つのグラフ上に表示させたい。 Rでは、2つのグラフを重ねる という操作をして、2つの異なるデータを1つのグラフ上に表示させる。
> plot(year,m_k, type="l") > plot(year,f_k, type="l")で描くことができる。
> plot(year,m_k, type="l")> par(new=T)
> plot(year,f_k, type="l")
> plot(year,m_k, xlim=c(1986, 2006), ylim=c(0,4000), type="l", lty=2)
ann=F, axes=F ##それぞれ、annは軸ラベル(xlabやylabで後ほど指定)、axesは軸目盛り
> plot(year,m_k, xlim=c(1986, 2006), ylim=c(0,4000), type="l", lty=1, ann=F, axes=F) > par(new=T) > plot(year,f_k, xlim=c(1986, 2006), ylim=c(0,4000), type="l", lty=2, xlab="Year", ylab="No. of death")
col="red"というオプションを追加
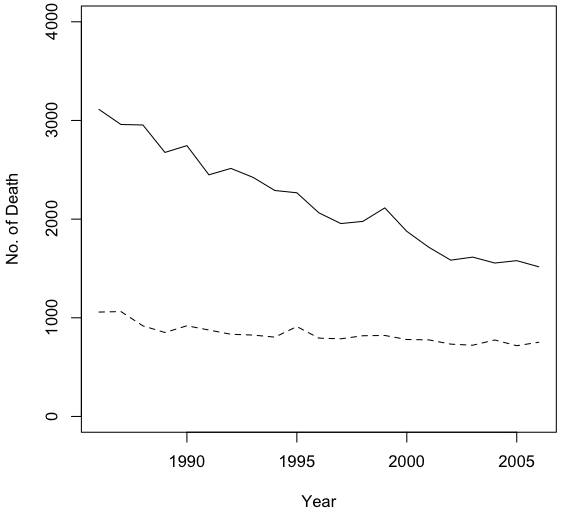
> plot(year,m_k, xlim=c(1986, 2006), ylim=c(0,100000), type="l", lty=1, ann=F, axes=F)
> par(new=T)
> plot(year,f_k, xlim=c(1986, 2006), ylim=c(0,100000), type="l", lty=1, ann=F, axes=F, col="red")
> par(new=T)
> plot(year,m_h, xlim=c(1986, 2006), ylim=c(0,100000), type="l", lty=2, ann=F, axes=F)
> par(new=T)
> plot(year,f_h, xlim=c(1986, 2006), ylim=c(0,100000), type="l", lty=2, xlab="Year",
ylab="No. of Death", col="red")plot(year,m_k, xlim=c(1986, 2006), ylim=c(0,4000), type="l", lty=1, ann=F, axes=F) par(new=T) plot(year,f_k, xlim=c(1986, 2006), ylim=c(0,4000), type="l", lty=1, col="red", xlab="Year", ylab="No. of Death") par(new=T) plot(year,m_h, xlim=c(1986, 2006), ylim=c(0,100000), type="l", lty=2, ann=F, axes=F) par(new=T) plot(year,f_h, xlim=c(1986, 2006), ylim=c(0,100000), type="l", lty=2, ann=F, axes=F, col="red") axis(4)
まず最初に参考書の紹介だが、Rには様々な参考書が出版されているので、どれか一冊を選んで買ってきて、随時参照しながら操作をするといいだろう。フリーのオンライン情報だけを使って使いたい人は、次のようにするといい。
1. Rの命令一覧が載っている説明書のPDF(上記)を画面に表示させる 2. Adobe Readerの検索機能を使って、行いたい処理を検索 3. 説明を読んで入力すべき命令文をコピー 4. Rにペーストして、値を編集して実行
こうやって、常に説明書を参照しながら操作すれば、命令を覚える必要は無い。
![[smile]](image/face/smile.png) †
†生物学を学ぶ限り、自分が実験や観察で得たデータを使うときに、統計解析は必ず使うことになる。生物学のための統計解析の本も、数多く出版されている。一年生の皆さんも、機会をみつけて、できるだけ統計学に慣れ親しんでおいて欲しい。そんなとき、Rは非常に役に立つ。Rは非常に強力な統計解析ソフトであるため、与えられたデータの持つ統計的特徴を瞬時に計算したり、データの持つ意味を推測するための図版を一瞬に作図してくれる。この授業ではRを使って実際にデータを解析することで、統計解析に慣れ親しむ方法を解説する。実際の理論的裏付けは、統計の本を読んだり、授業に出たりして、各自学習してほしい。
この授業では統計解析を、次の2つの目的のために使う。
1. ある対象(母集団)から得られた部分的な数値データから、その対象の持っている性質や特徴を知ること
2. ある対象や実験で得られた数値データを用いて、その対象についてどういう判断を下せば良いかを論じること
"ある対象(集団)から得られた部分的な数値データから、その対象の持っている性質や特徴を知ること"
っていうけれど、「母集団」って何?
「母集団」というのは、興味の対象になっている集団全体のことだ。
例えば、
生物学の大きな目的の一つに、自然界に存在する様々な生物の特徴を知ることがある。しかし、自然界の全ての生物個体を計測して、特徴を知ることは不可能。そこで、対象とする生物から、一部だけ(標本)を偏り無く取り出して(これを任意抽出とかランダムサンプリングと呼ぶ)、特徴を計測し、対象生物全体(母集団)の特徴を推定する。こういう作業を「統計的推測」と言う。
この、「一部を使って全体を知る」という点が、統計の基本!
生態学などのマクロ系の生物学では、上のような方法で標本を採集し、母集団の性質の解析に統計学的手法を用いることが、非常に多くある。この授業では、統計学全般について語っている時間は無いので、ほんのさわりしか扱わないが、下に示す参考書などを読んで、勉強しておいて欲しい。受験で培った数学力が落ちておらず、学問に対する情熱が非常に高い、1年生の今が統計学習得のチャンスですぞ!
それでは、実際に統計的推測やってみよう。。
【ここをクリック】←ここに、産業技術総合研究所 デジタルヒューマン研究センターから提供して頂いた、1997年の男子大学生110人の身長、体重のデータがある(表示されない人は、moodleページを見てみよう)。このデータを使って、1997年当時の大学生の身長と体重の一般的傾向について議論してみよう。
このとき、
母集団は1997年当時の大学生全て
標本は1997年の男子大学生110人
標本母集団からランダムに(無作為に)抽出されたとする
今回の統計的推測では、
110人分のデータから、1997年当時の大学生全体の身長と体重の傾向を推測する
ことを目的としている。
> h=scan() 1:画面に表示された 1: の後に、上のページから身長データをコピー・ペーストして、最後にenter キーを押す。次のように表示される。
1: 1775 1710 .. ..<省略>.. 111:同様にして、体重データも w というオブジェクトにを入れる。次のように表示される。
1: 79.8 58.0 .. ..<省略>.. 111:確認のために
> h > wと入力。データが一覧表示される。
計測データが得られたら、まずは、グラフにしてみるよう。グラフとして視覚化することで、データの持つ性質が直観的に理解できる。こういうとき、Rは、いろんなグラフを一瞬にして描画してくれるので、非常に便利。
まずはヒストグラム(柱状グラフ)を使っみる。Rを使ってヒストグラムを書く場合は
> hist(h)キーボードからたった7文字打ち込むだけで、身長の度数分布がグラフで表示される。
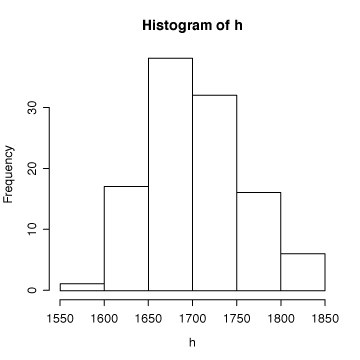
このグラフを見ただけで、標本データでは身長170cmぐらいの学生が最も多く、 データは釣り鐘型の分布をしているということが分かる。同様のことを体重についてもやってみよう。
> hist(w)
次に、この標本データの平均とか最大値とか、最小値とか、データの集まりがもっている基本的な性質を表示させて見よう。次のように入力。
> summary(h) Min. 1st Qu. Median Mean 3rd Qu. Max. 1578 1671 1700 1706 1734 1839これで、1997年当時の調査した大学生110人の身長は、平均170.6cm(最大:183.9cm, 最小: 157.8cm)ということが分かった。1st Qu.と3rd Qu.というのは、全体の4分の1の人数(つまり25%)がどの高さまでの間に含まれているかということを表している。つまり、167.1cm以下の人が25%、173.4cm以上の人が25%、その間の人が全体の50%ということ。
> summary(w)
身長も体重も釣り鐘型の分布になっていた。では、この2つの数値の間に何か、関係があるだろうか?これもまた、グラフで表示させてみる。こういう場合、縦軸に体重、横軸に身長をとって、一人一人の持つ身長と体重の散布図を作る。Rの場合、次のように入力するだけ。
> plot(h,w)身長と体重の関係は右上がりの直線関係にありそうだ。
>cor(h,w) [1] 0.5872979 #値が正なら正の相関
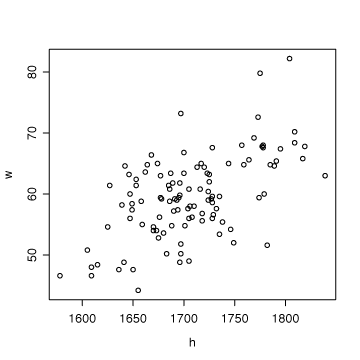
今回、110人分のデータを使って、1997年当時の大学生男子の身長と体重について、
グラフによる視覚化 要約統計量の表示 散布図の作成という3つのことを行った。この標本が母集団の性質を表しているとするならば、1997年当時の大学生について、次のような推定ができる。
1997年当時の男子大学生は、身長の平均が170.6cmで、データは釣り鐘型に分布している 体重は平均が59.53kgで、身長と同様にデータは釣り鐘型に分布している 身長と体重の間には、正の相関があるこれで、1997年当時の男子大学生という母集団の身長・体重について、統計的推定を行うことができた!
なお、今回は分散や標準偏差の話しは省略した。Rを使った統計解析の基本(データの図示、代表値の計算、データ間の相関)などについてはここでは説明しきれないので、下のリンクにある中澤さんによる解説などを読んで、勉強してみて欲しい。。