![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
前回授業でやった仮説検定のところがよくわからなかったという意見が多かったです。そこで、正確さは二の次にして、仮説検定で行っている作業をイメージで理解してもらえるようまとめてみました。それぞれどこの部分が、帰無仮説、有意水準、帰無仮説の棄却にあたるのか考えてみてください。また、なんとなく理解できたら、統計の教科書を読んでみることを強くお勧めします。1年生の今が、統計学を勉強するチャンスですぞ!!
1枚のコインを20回投げたら、オモテが5回しかでなかった。このコインはいかさまコインかなー?
もし、このコインがいかさまコインじゃない(正常なコイン)とすると...
20回中5回しかオモテが出ないのっていうのも、わりとフツーに起こることなんだろーね。
わりとフツーに起こるこってどうやって数字で示す?確率で 95パーセントぐらいかな?...
まともなコインで20回中のオモテの数ごとに、それが起こる確率をグラフにしてみると...
なんと!!95パーセント以上っていうのは、オモテの数が6枚から14枚までの場合だっ!
オモテの数が5枚の場合は、5%の範囲というフツーじゃ起こらないとした範囲に含まれちゃってる...
「20回中5回しかオモテが出ない」っていうのが、「正常なコイン」では滅多に起こらないっていうわけだから、このコインが「正常なコイン」っていう前提が間違っていたと考える方がいいんだろうね。
うん、きっとこのコインは、いかさまコインなんだ
でも、待てよ。フツーじゃ起こらないことの判断基準が5%って大きすぎない?
5%っていうと、、、100回中5回。。。 20回中に1回だ!
さっきのいかさまコインっていう判断も、この判断基準の大きさによっては間違ってるのかもしんないね
> binom.test(15,20)
Exact binomial test
data: 15 and 20
number of successes = 15, number of trials = 20, p-value = 0.04139
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.5089541 0.9134285
sample estimates:
probability of success
0.75
前回の授業で使ったRという計算ソフト。コマンドを入力するのはちょと難しいけど、エクセルみたいにマウスを使って面倒な操作をしなくても、一瞬にしてグラフが描けてしまう優れものです。これなら、良いレポートを仕上げるために、何度も解析をやりなおして、グラフを描き直すっていう作業も面倒ではなさそう。。。
初めて使ったソフトなのに、皆さん、けっこうRの操作には慣れているし(ほとんどみんな、課題ができていた)、面白さも感じてくれたよう。そこで、今回はやってみたいという要望の多かったプログラミングをRを使って勉強します。
前回やったRを使った計算のおさらいを、サンプルデータをつかってやってみましょう。
下のデータは仲岡先生の実習でやった、調査コドラートの面積と、出現種数です
コドラート1 10*10 2種 コドラート2 15*15 4種 コドラート3 20*20 7種 コドラート4 25*25 7種 コドラート5 30*30 7種 コドラート6 35*35 9種 コドラート7 40*40 8種 コドラート8 45*45 12種 コドラート9 50*50 10種 コドラート10 55*55 10種 コドラート11 60*60 11種 コドラート12 65*65 11種 コドラート13 70*70 9種 コドラート14 80*80 10種 コドラート15 100*100 12種 (データ提供、してくれた方に感謝!)
Rを使ってこのデータの、面積と種数の相関関係を知りたいとき、必要なのは、コドラートの1辺の長さと種数のベクトルです。
今から何をするか、もうお分かりですよね?
予想通り、K2Editorを立ち上げて、要らないところを消し、
10 2 15 4 . .
というデータに整形して、エクセルにコピペして、1列ごとのデータを scan() 関数を使ってオブジェクトに読み込みます。では、やってみましょう。(そろそろミミタコだろうから、説明は簡単に書いておきます)
検索文字列: ^.*\* (説明:行頭から最初のアスタリスクまで) 置換文字列:<無し>(つまり削除するということ) 検索文字列: 種 置換文字列:<無し> 検索文字列: + (説明:左に書かれているのは半角のスペースと半角のプラス) 置換文字列: \t (説明:タブ)
10 2 15 4 . .
> q=scan() [1] ← ここでペースト。yについても同様 > y=scan()
> q [1] 10 15 20 25 30 35 40 45 50 55 60 65 70 80 100 > y [1] 2 4 7 7 7 9 8 12 10 10 11 11 9 10 12
x=q^2
![[smile]](image/face/smile.png) )
)
> plot(log10(x), log10(y))
> result=lm(log10(y) ~ log10(x)) > result Coefficients: (Intercept) log10(x) -0.1375 0.3250 ここに表示された結果は、log(y)=0.325*log10(x)-0.1375 という回帰直線の式
> abline(result)
> summary(result)
Call:
lm(formula = log10(y) ~ log10(x))
Residuals:
Min 1Q Median 3Q Max
-0.211429 -0.054045 0.006334 0.053616 0.142160
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.13750 0.15254 -0.901 0.384
log10(x) 0.32498 0.04713 6.896 1.09e-05 *** ←有意水準0.1%で有意
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ←これ、有意水準
Residual standard error: 0.09927 on 13 degrees of freedom
Multiple R-Squared: 0.7853, Adjusted R-squared: 0.7688
F-statistic: 47.55 on 1 and 13 DF, p-value: 1.092e-05 > cor.test(log10(y),log10(q2))
Pearson's product-moment correlation
data: log10(x) and log10(y)
t = 6.8957, df = 13, p-value = 1.092e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.6847590 0.9618161
sample estimates:
cor
0.886173 ← 相関係数この授業では、それぞれの分析の意味については説明しません。仲岡先生に聞いて下さい。(グラフ用紙で提出しなくてもいいと仰っていたような、いなかったような。。。)
*大事なこと*
「こんな解析、自分でやるのは絶対無理!」と思うかもしれませんが、 そんなことは無いです!
上のような解析の方法、私だってRでできるとは知りませんでした。 では今回、私はどうやったのでしょう?「回帰分析行いなさい」なんて言われたら、どうすればいいのでしょうか?もしかしてRでできるかなと思ったら、
Adobe Readerを使って、マニュアルを検索します
ところで、プログラミングって何をすることでしょうか?IT用語辞典で調べてみると、、、
載っていません
唯一近いところでは、「プログラミング言語」というのがあります。説明文からプログラミングに関わるところを抜き出して、「プログラミング」の説明文を作ってみると、
今日の授業でコンピュータにあれこれ命令を与えるために使うRは、計算ソフトですが、インタプリタ型のプログラミング言語ということもできます。
つまり、プログラミングとは、簡単に言うと、「言葉を使ってコンピュータが理解できる命令を作ること」 です。
「Wordを立ち上げて文章を作成し、印刷する」とか、「Excelで家計簿を管理する」とかは、市販のソフトウェアを使った作業ですが、いずれも、非常に高度で複雑な命令が、使用者からコンピュータに向かって発せられています。マウスを動かしたらポインタが動くなんていうのは、けっこう複雑な命令ですよ。でも、ほとんどの場合、一般の人がコンピュータでやりたいと思うほとんどの作業は、わざわざ「命令」なんていうものを意識する必要は無いはずです。利用者が理解しやすく・使いやすいように、専用のソフトウェアが開発され、販売されているでしょう。
生物学の研究者でも、プログラミングなどを経験したことの無い人は大勢います。だって、今や、DNAシーケンスの決定や、整列や、系統樹作成にだって、専用のソフトウェアがあるのですから。。。それぞれのソフトウェアの使い方を覚えれば、それですむわけです。私たちも新しい解析方法が開発されるたびに、そのソフトウェアの使い方を覚えるのに苦労しています。
でも、それだけで、本当にいいのでしょうか?良くないという点が、まず、2つ思いつきます。
1. 自分の目的にあったソフトウェアがいつも存在するというわけではない 2. ソフトが存在する場合、目的の数だけ、ソフトの使い方を覚えなければならない
ということです。特に1番目は致命的ですね。ソフトウェアが開発されてなかったら、目的が達成できないのですから。例えば、集団遺伝学で学ぶ、遺伝的浮動の解析ソフトなんていうのは、パソコンショップに行っても売ってないです(でも、じつは、このくらいメジャーなものなら、ネットで探せばフリーのものがあります)。
そこで、この授業でプログラミングを勉強する理由は次の3点です。
「Hello World!」だなんて、なんか変なタイトルだなーと思いますよね。誰が使い始めたのかは知りませんが、様々なプログラミング言語の教科書で、最初に出てくるのがこのプログラミングです(プログラムを勉強したことのある人なら、たいてい誰でも知っています)。では、早速やってみましょう。Rを立ち上げて、次のように入力してください。
print("Hello World!")
うまくご挨拶できましたか?
ここでやったのは、print()という関数を使って"Hello World!"と画面に表示させただけですが、これも
画面にHello Worldと表示させる
ということを目的としたプログラミングです。
えっ?それなら、Rの最初でやったオブジェクトの内容を画面に出すのもプログラミング?
と聞かれるかもしれませんが、その通りです。次の囲みの中を全てコピーして、Rのコンソールにペーストしてみましょう。
x=c(1,2,3,4,5,6,7,8,9,10) sum(x)
上でやったプログラミングは、
画面に1から10までの整数の合計を表示させる
というプログラミングです。皆さんがこれまでにやってきたRを使った操作も、何らかの処理の結果を画面に表示させるプログラミングだったわけです。なんとなく、プログラミングが身近になったでしょ?
上でやった2つのプログラミングですが、違いがありますね。"Hello World!"の方は1行だけの命令だし、合計値の方は2行になっています。プログラムは通常、いろんな処理を組み合わせて作るので、複数行になることが多いです。次に3行からなるプログラミングをやってみましょう。
q=c(10,15,20,25,30,35,40,45,50,55,60,65,70,80,100) y=c(2,3,4,5,6,7,8,9,10,11,10,11,9,10,12) plot(log10(q^2), log10(y))
このプログラムは、
2つの数値ベクトルについて計算を行って、対数グラフを描く
というものでした。さっき、上でやったのと同じことを、複数行にまとめて書いて、まとめてRに命令したわけです。
授業では一つ一つ解説しますが、復習課題をやるときとか、自分で新たな解析に挑戦するときは、どういう命令があるかが書かれた説明書が必要になるでしょう。
> ?plot > example(plot)という風に、?の後に関数名を打てば、説明や使用例が英語で表示されます。説明文の一番最後にはExample(使用例)が載っていますので、けっこう参考になります。
上で複数の行で様々な命令を一度にRに与えられるということを解説しました。でもやったことは、それぞれ個々の計算を順番に並べて、一度にペーストしただけですよね。そこで、次にもっとプログラムらしい命令をRに与えてみましょう。それは、繰り返しと代入と条件分岐というもので、プログラミングの基本中の基本です。
人が不得意でコンピュータが得意なことの一つは、単純な繰り返し作業を際限なく(文句も言わずに)行うことです。要するに、プログラミングの一つの目的は、そういう面倒な繰り返し計算をコンピュータにやらせることです。では、何回繰り返すかというのをどうやってコンピュータに指示するかというと、forという命令を使います。
for(i in 1:10) { print(i) }
この命令は、
{ } で囲まれた部分の命令を10回繰り返しなさい
というものです。
{ } の中は何をする命令か分かりますか?
では、やってみましょう。1から10までの整数が表示されましたね。ここでもう一度命令文をよく見てみましょう。
for と (i in 1:10) と { print(i) } に分かれています
for は これから繰り返し命令が始まるよということを示しています
(i in 1:10) は 繰り返しの回数が10回であることを示しています
つまり、50回繰り返したかったら (i in 1:50) とします
iという文字の代わりに、jでも、kaisuでも、構いません
{ print(i) } は iという変数の値を画面に表示させなさいという意味ですというものです。 { } のところは複数行に分かれていてもよく
for(i in 1:10) {
print(i)
}
と書いても結果は同じです。
練習問題: 2から18までの偶数を全て表示させるプログラムをfor命令を使って作りなさい
解答例:(穴埋め形式)
for(i in _:_){ # _ のところには数字が入ります
print(i*_)
}上の for(i in 1:10) { print(i) } というプログラムでは、iの値は繰り返しの度に違う値になります。
1回目 iの値は1 2回目 iの値は2 3回目 iの値は3 .... ........ 10回目 iの値は10
では、一つ前の繰り返しの時のiの値を使いたい場合はどうすれば良いでしょうか?例えば、1から10までの合計をfor命令を使ってプログラミングすることを考えると、
今の繰り返し回数のiの値に1つ前回数までの合計を加えて表示させたい 1回目 iの値は1 1つ前までの合計は0 1 を表示 2回目 iの値は2 1つ前までの合計は1 3 を表示 3回目 iの値は3 1つ前までの合計は3 6 を表示 .... ........ 10回目 iの値は10 1つ前までの合計は45 55 を表示
こういう場合に代入という命令を使います。その命令は
=
です。通常の計算では'='というのは「3+5=」というように、計算を行わせる意味で用いられますが、プログラミングにおいては、
左辺の変数に右辺の計算結果を代入する
という意味で用いられます。上の計算のプログラムは次のようになります。
goukei=0 #goukeiという変数に初期値0を代入
for(i in 1:10) { #以下を10回繰り返す
goukei=goukei+i #goukeiに前回までのgoukeiの値にiの値を足したもの代入
print(goukei) #goukeiの内容を画面に表示
}
goukei=goukei+iという命令文では、右辺の「goukei+i」を先に計算して左辺の「goukei」に代入しているところが、分かりにくいかもしれません。
練習問題: 1から10まで累積してかけ算をした結果を全て表示させるプログラムを作りなさい
seki=_ #sekiという変数に初期値1を代入(かけ算だから)
for(i in 1:10) { #以下を10回繰り返す
_=_*_ #sekiに前回までのsekiの値にiの値を掛けたもの代入
print(seki) #sekiの内容を画面に表示
} seki=1 #sekiという変数に初期値1を代入
kekka=c() #kekkaというオブジェクトに空ベクトルを初期値として代入
for(i in 1:10) { #以下を10回繰り返す
seki=seki*i #sekiに前回までのsekiの値にiの値を掛けたもの代入
kekka=append(kekka,seki) #kekkaというベクトルにsekiの値を要素として追加
}
print(kekka) #kekkaの内容を画面に表示
kekka=append(kekka,seki)とgoukei=goukei+iという2つの式はよく似た働きをしています。
kekka=append(kekka,seki) kekkaにsekiを要素として追加したものをkekkaに代入 goukei=goukei+i goukeiにiを加えたものをgoukeiに代入
seki=1 #sekiという変数に初期値0を代入
kekka=c() #kekkaというオブジェクトに空ベクトルを初期値として代入
for(i in 1:10) { #以下を10回繰り返す
seki=seki*i #sekiに前回までのsekiの値にiの値を掛けたもの代入
kekka=append(kekka,seki) #kekkaというベクトルにsekiの値を要素として追加
}
print(kekka) #kekkaの内容を画面に表示
plot(log10(kekka)) #kekkaの対数をグラフにプロットずいぶんとプログラムらしくなってきました
#**次のプログラムの実行結果を予測してください。**
for(i in 1:9) { #iの値を1から9まで1ずつ変化させる
for(j in 1:9){ #jの値を1から9まで1ずつ変化させる
print(i*j) #iとjを掛けたものを表示する
}
}result=c() #resultに空ベクトルを初期値として代入
for(i in 1:9) { #iの値を1から9まで1ずつ変化させる
for(j in 1:9){ #jの値を1から9まで1ずつ変化させる
result=append(_, _) #iとjを掛けたものをresultの要素として追加
}
}
matrix(result, nrow=i, ncol=j) #nrowとncolはそれぞれ行の数、列の数を示す
#iとjはそれぞれ9で終わっているので、9x9のマスになる
> result
プログラミングの基本技の最後は1つは条件分岐です。if()を使って表現します
i=3 #iに3という数値を代入
if(i==3){print("三")} #iの値が3ならば画面に三と表示
この例の2つめのif命令で、iの値を評価しています。評価に使われるのは比較演算子というもので、
== 等しければ != 等しく無ければ >, >= 左辺が右辺よりも大きければ、左辺が右辺以上ならば <, <= 左辺が右辺よりも小さければ、左辺が右辺以下ならば
ということを意味しています
という命令です。{}の中は複数行にわかれていてもよく、また、else を使えば、それ以外の条件を指定できます
i=4
if(i==3){
print("san")
} else {
print("san deha nai")
}
では、上の繰り返しと条件分岐を組み合わせて見ましょう
1から10までのうち、5以外を画面に表示しなさい
というプログラムなら
for(i in 1:10){
if(i != 5) { # != は「等しくない」ということを示します
print(i)
}
}
では、次のプログラムを作ってみてください
1から10までの数字を表示させなさい、5だけは"five"と英単語で表示させなさい
右の図は見たことがあるでしょ?これは、遺伝的浮動の効果を説明するときによく使われるグラフです。このシミュレーションでは、集団サイズN=100, 2つの対立遺伝子のうち、片方の対立遺伝子の頻度を示す。最初の世代の対立遺伝子の数は50:50。このグラフを使って、遺伝的浮動とはどういうものか、説明できる人はいますか?また、このグラフはどうやって作ったものですか?
こんな図を作るのはとうてい無理と思っちゃうかもしれません。でも、Rを使ってプログラミングすると、わりと簡単に描けてしまいます。
今回は、Rを使ったプログラミング体験の到達目標として、「遺伝的浮動」のシミュレーションをやることにしました。このテーマを選んだ理由は、「生物学科の皆さんになじみが深い」、「Rをつかってやってみて見た目が面白い」、「思ったよりはプログラミングが簡単」というこです。さらに、私にとっては初めて自分で挑戦したシミュレーションで、できあがったグラフを見たときにはかなり嬉しかったものです。
なお、シミュレーション(simulation, 「シュミレーションでは無いですよ!」)は、数学モデルなどを用いて現実に似た状況をコンピュータ上で再現することです。模擬実験とも呼ばれています。(大量の計算を必要とするので、Rのようなインタプリタ型のソフトでは、大規模なシミュレーションは難しいです)
これからシミュレーションを行うのですが、つぎのような状況を想定してみましょう。
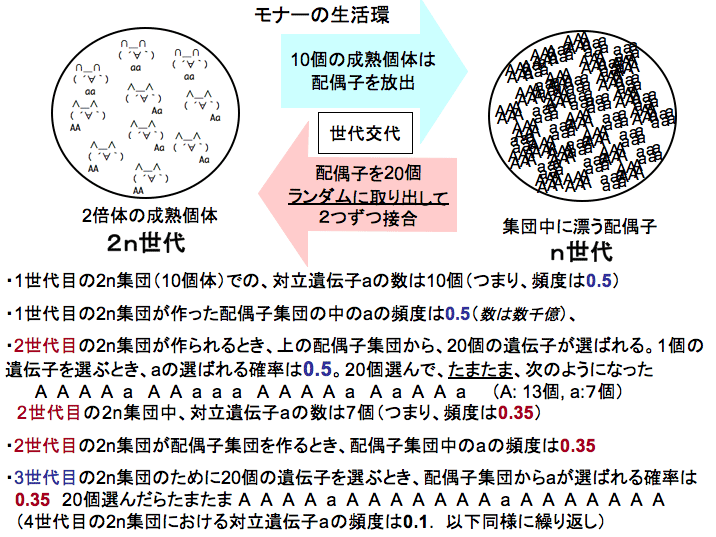
まず、対象とする架空の生物(仮に、「モナー」と呼びます(注:モナーについて詳しく知りたい人は、ウィキペディアで「モナー」を検索してみてください。))は2倍体の生物で、雌雄の区別が無く、繁殖期になると集団内の個体が一斉に配偶子を数千億個ずつ放出して死亡します。配偶子は生息域の空間内をランダムに漂った後、24時間後に、最も近くにある配偶子と接合し、新しい繁殖個体になります。集団の生息域は空間的に限られているため、親世代と同数の子供個体しか、成熟個体になれません。どの子供が成熟個体になるかは、ランダムに決まるものとします。つまり、このモデルだと、世代間で集団サイズに変動は無いということです。モナーにはトンガリ耳と丸耳の2タイプが1対立遺伝子(A, a)で決まることが知られています。トンガリ耳の遺伝子型は(AA, Aa)、丸耳の遺伝子型は(aa)です。
なお、上のモナーの説明は、私が今回のシミュレーションのために、適当に設定したものです。だって、「任意交配をする有限サイズの生物集団から遺伝子をランダム抽出して、同サイズの次世代集団を作った」なんて言い方をするよりは、生物を扱ってる感じがするでしょ?
モナー10個体からなる、1つの集団を考えてみましょう。いまこの集団で、対立遺伝子Aの頻度が0.5, 対立遺伝子aの頻度が0.5のとき(10個体だから遺伝子の総数は、20個です。そのうち半分の10個がAで、10個がaです)。集団中の配偶子の接合はランダムに起こると仮定して、100世代の間に、集団中の対立遺伝子の頻度はどのように変化するでしょうか?
今から実験をするのですから、前もって予想しておいた方が面白そうです この集団の遺伝子頻度が1か0に固定するまでに、何世代ぐらいかかると思いますか?
a=c(10) #対立遺伝子aの集団中の個数
for(i in 1:30){ #この行から対応する}までの間を 100世代分繰り返す
counta=0 #次世代にランダムに残るaの値を入れる変数を初期化
for(j in 1:20){ #数千億からなる配偶子プールから1個の配偶子を取り出す試行を20回行う
if ( runif(1) < ??? ){ # *** 取り出した遺伝子がaだったならば ***
counta=counta+1 # *** aの個数を入れる変数の値を1増やす ***
}
}
out=counta/20) #何世代目かという数字(i)と対立遺伝子aの頻度(a/20)をoutというオブジェクトに入れる
print(out) #outの内容を画面に表示する
a=counta # aの値を新しい世代の対立遺伝子aの個数(counta)で置き換える
}
上から順番に意味を考えてゆきましょう。
それでは、次のプログラムを走らせて、20個の遺伝子中対立遺伝子aが10個ある任意交配集団の、100世代の間のaの遺伝子頻度の変化をみてみましょう。
a=10 #対立遺伝子aの集団中の個数
for(i in 1:100){ #この行から対応する}までの間を 100世代分繰り返す
counta=0 #次世代にランダムに残るaの値を入れる変数を初期化
for(j in 1:20){ #数千億からなる配偶子プールから1個の配偶子を取り出す試行を20回行う
if ( runif(1) < a/20 ){ #乱数を一つ発生させ、それが対立遺伝子aの頻度(a/20)よりも小さければ
counta=counta+1 #aの個数を入れるcountaという変数の値を1つ増やす
}
}
out=c(i, counta/20) #何世代目かという数字(i)と対立遺伝子aの頻度(a/20)をoutというオブジェクトに入れる
print(out) #outの内容を画面に表示する
a=counta # aの値を新しい世代の対立遺伝子aの個数(counta)で置き換える
}
さて、皆さんの計算結果はどうでしたか?何世代目で固定された?
全ての課題は、http://bean.bio.chiba-u.jp/joho18/ に、「自分のID/10」という新しいページを作成し、これまでの提出例にならって、分かりやすく書き込むこと。あまりに分かりにくい回答は減点します。
下の囲みの中にあるアンケートをコピー・ペーストして、「回答:」の後に答えを書き込むこと。
*第10回授業アンケート **氏名: **課題への回答 -今日(6月22日)の授業の進み方は?(はやい、丁度いい、おそい) --回答: -今日の授業の難しさはどう感じましたか(簡単すぎ 簡単 丁度いい 難しい 難しすぎ): --回答: -難しいと答えた人は、特にどの点が難しかったですか?: --回答: -今日の授業は(よく分かった 分かった 分からなかった): --回答: -分からないと答えた人は、特にどの点が分からなかったですか?: --回答: -今日の講義で理解できなかった用語があったら挙げてください: --回答: -Rで何ができるのか、だんだん分かってきたと思います。今後自分の勉強にRを使うつもりですか? --回答: -Rでも、R以外の言語でも、何かやってみたいプログラミングはありますか? --回答: -今回やったプログラミングはおもしろかったですか? --回答:
次の問題文の指定にあるプログラムを作成しなさい。作成したプログラムは課題提出ページに貼り付けなさい。 行頭には必ず半角の空白を入れること。
以下の設問に答えなさい
<font size="16"><i><b>HTMLの世界にようこそ!</b></i></font>
**素朴な疑問** 「こういうシミュレーションのプログラミングって、これから生物学を学ぶのに、どのくらい必要なんですか?」 ==おへんじ= 画一的な答えは難しいです。シミュレーションそのものが直接必要になるような分野もあれば、そうでない分野もあります。 ただ、私は、プログラミングは、生物学における発展的な情報処理をする上での基本技だと考えています。 千葉大の研究室に限って言えば、プログラミング技術が無いと卒業研究が終わらないというところは 現時点では(たぶん)無いでしょう。但し、プログラミングができると、卒業研究や修士の研究でより 進んだことができたり、理解が深まったり、研究が楽になるようなところはいくつもあります。 数理生物学、理論集団遺伝学、進化生態学、バイオインフォマティクスを志す人には、 敢えて、不可欠な技術だと言っておきます。
それでは、次のプログラムを走らせて、20個の遺伝子中対立遺伝子aが10個ある任意交配集団の、100世代の間のaの遺伝子頻度の変化をみてみましょう。
numa=10 #対立遺伝子aの集団中の個数
for(i in 1:100){ #この行から対応する}までの間を 100世代分繰り返す
counta=0 #次世代にランダムに残るaの値を入れる変数を初期化
for(j in 1:20){ #数千億からなる配偶子プールから1個の配偶子を取り出す試行を20回行う
if ( runif(1) < numa/20 ){ #乱数を一つ発生させ、それが対立遺伝子aの頻度(a/20)よりも小さければ
counta=counta+1 #aの個数を入れるcountaという変数の値を1つ増やす
}
}
out=c(i, counta/20) #何世代目かという数字(i)と対立遺伝子aの頻度(a/20)をoutというオブジェクトに入れる
print(out) #outの内容を画面に表示する
numa=counta # aの値を新しい世代の対立遺伝子aの個数(counta)で置き換える
}
前回、全角の空白が混じっていたため、うまく動かなかったプログラムがこれです。まず、これを始めに動かしてみて、 もう一度、プログラムの内容を理解してゆきましょう。
前回のレポートで、コピー・ペーストすれば動くのはわかるけど、どうやったらこういうのが作れるのか分からないという意見がありました。私としては、クラスのほとんどの人に、プログラミングとはどういうことをするものかを分かって欲しいので、作成過程を1つずつ、順を追って説明します。
20個の遺伝子からなる集団 0世代目の対立遺伝子aの数が10(つまり対立遺伝子aの頻度は0.5) この集団を100世代観察するという条件にしておく
*自分で考えた変数名と定数
numa=10 #0世代目の対立遺伝子aの数。2世代目以降は、シミュレーション実験で抽出されたaの数が代入される
counta=0 #配偶子プールから、次世代の集団に取り出された対立遺伝子aの数。1世代が終わったあとで、
数字が入るので、とりあえず今は0を入れておく
20 #集団の大きさ(つまり、集団に含まれる遺伝子の数)
100 #繰り返しの世代数

*自分で考えたプログラムの構造。コマンドを使って書かなくても、 とりあえず、構造が理解できるように書いてあればよい。

*100回繰り返す繰り返し文の構造
for(i in 0:100) {
<※ここに繰り返される内容が入る>
}※集団中の遺伝子数分、つまり、20回繰り返す文
for(j in 0:20) {
<※※ここに繰り返される内容が入る>
} ※※の操作:
「配偶子を一つ取り出すとき、遺伝子頻度の確率で、対立遺伝子aをひく。もし、対立遺伝子aを引いたら、
aの数を入れておく変数(counta)の値を1つ増やす」
= 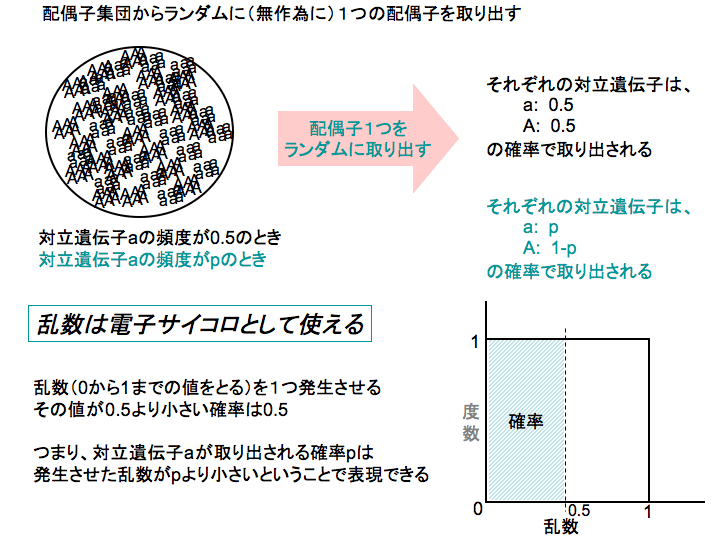

上の『対立遺伝子aを引いたら』(このことは対立遺伝子頻度aの確率で生じる)というのは、
『乱数を一つ発生させたとき、それが対立遺伝子頻度aより低かったら』(これも対立遺伝子頻度aの確率で生じる)と
同じことと考える。そこで、
「乱数を一つ発生させたとき、それが対立遺伝子頻度aより低かったら、
aの数を入れておく変数(counta)の値を1つ増やす」
・内側のfor文の繰り返しが1回終わったら numa = counta counta = 0
これでは使いにくいので、aの値を自由に変更できる関数を定義してみましょう。「関数の定義」なんていうと難しそうですが、ようするに、作ったプログラムに名前をつけて、いろいろと数値を変えて解析できるようにすることです。
drift1=function(a){ #関数定義の始まり
#上にあった、a=10 という命令は削除。この関数では、aの値を自由に変えられる
for(i in 1:30){
counta=0
for(j in 1:20){
if ( runif(1) < a/20 ){
counta=counta+1
}
}
out=counta/20
print(out)
a=counta
}
} #関数定義の終わり
さっきのプログラムの上下を関数を定義する関数であるfunction(){}で囲んで、オブジェクトに代入するだけですから、簡単です。この関数を実行するには、最初aの値を()の中に入力して、
drift1(10)
とします。
↑を使って何回も実行してみると、結果がいろいろ変わるのがわかりますよね。
では、せっかく結果が出たのだから、グラフにしてみましょう。でも、その前に、以前使ったplot()という関数を思い出してみましょう。
x=c(1,2,3,4,5) plot(x)
plot()という関数は、ベクトルの内容をプロットしてくれるのでした。そうすると、今のdrift1関数の実行結果はどうやれば表示できるでしょうか?
関数を実行した結果が全て、一つのオブジェクトにベクトルとして格納されていれば良い。例えば: 0.6, 0.55, 0.65, 0.8, 0.95, 1, 1, 1, ...
これをやるには、上のout=count/20としているところを、次から次へとベクトルの要素を付け加えるようにすれば良さそうです。ベクトル要素を付け加える関数が
append()
です。
results=append(results, a/20)
と書けば、resultsというベクトルにa/20の値が追加されます。但し、ひとつだけ重要な注意があります。
resultsというベクトルはあらかじめ存在していなければ、append()は使えない
つまり、for文を使って繰り返しを行う前に、
results=c()
という命令で、空ベクトルを作っておく必要があるのです。
では、まず、結果をresults()に入れてベクトルで返すような変更を、上のプログラムに加えて見ましょう
drift2=function(a){
results=c() #空ベクトルを作る
for(i in 1:30){
counta=0
for(j in 1:20){
if ( runif(1) < a/20 ){
counta=counta+1
}
}
results=append(results, a/20) #ここにあった out=counta/20 の代わりに、append()関数でベクトル作成
a=counta
}
print(results) #printの文はfor文の外に出したことに注意!理由は分かりますよね
}
これで
[1] 0.50 0.60 0.80 0.70 0.55 0.50 0.35 0.40 0.20 0.30 0.1....
というベクトルが表示できました。これをplot()でグラフにするには、
plot(drift2(10))
とやるだけです。
しかし。。。ちょっと待てよ?どうせなら、関数の中にplot()を入れてしまえばすぐにグラフが表示されるのでは?
drift3=function(a){
results=c() #空ベクトルを作る
for(i in 1:30){
counta=0
for(j in 1:20){
if ( runif(1) < a/20 ){
counta=counta+1
}
}
results=append(results, a/20)
a=counta
}
plot(results) #ここにあった print文の代わりに、plot()でグラフ表示
}
グラフがすぐに表示できました!でも、点々では見にくいので、線で結んでみましょう。plot()のところを、
plot(results, type="l")
とかえるだけです。
drift4=function(a){
results=c() #空ベクトルを作る
for(i in 1:30){
counta=0
for(j in 1:20){
if ( runif(1) < a/20 ){
counta=counta+1
}
}
results=append(results, a/20)
a=counta
}
plot(results, type="l") #ここにあった print文の代わりに、plot()でグラフ表示
}
上で作ったプログラムを何度も走らせてみると、グラフの形がどんどん変わります。これはこれで面白いのですが、グラフの軸が一定していないし、1つのグラフに結果が重ねて表示されないので、ちょっと感じがつかめませんね。
そこで、いっそのこと、この実験を20回ぐらい繰り返してみて、結果を1つのグラフに表示させることにしましょう。同じことを何度も繰り返すのですから、for文をもう一つ、外側に作ればいいって、容易に想像がつきますよね?
drift5=function(a){
for(i in 1:20){ #これまでのプログラムの外側に新しく作ったfor文。20回繰り返す。
results=c()
for(j in 1:30){
counta=0
for(k in 1:20){
if ( runif(1) < a/20 ){
counta=counta+1
}
}
results=append(results, a/20)
a=counta
}
plot(results, type="l")
} #新しく作ったfor文の終わり。ここまで繰り返し。
}
さあ、走らせてみましょう。
drift5(10)
あれ?なんか変ですね。最後は0.0で線が一本でるだけです。
なぜだか分かりますか?
こたえは、aの値です。最初、aは10で与えられましたが、1集団分の繰り返しが終わった後、次の繰り返しの前に、下の数字に戻すのを忘れていました。
drift5=function(a){
firsta=a #関数に渡された(つまり()の中に書かれた)aの値をfirstaというオブジェクトに保存
for(i in 1:20){ #これまでのプログラムの外側に新しく作ったfor文。20回繰り返す。
a=firsta #繰り返しの最初に、aの値を初期値(firsta)に戻す
results=c()
for(j in 1:30){
counta=0
for(k in 1:20){
if ( runif(1) < a/20 ){
counta=counta+1
}
}
results=append(results, a/20)
a=counta
}
plot(results, type="l")
} #新しく作ったfor文の終わり。ここまで繰り返し。
}
できました。実行してみましょう。ウーン。。。うまくいってるようなのですが、1回ずつ、グラフが変わっちゃいます。グラフを重ねて描くには、par(new=T) というコマンドをplot()の前に使います。
drift5=function(a){
firsta=a #関数に渡された(つまり()の中に書かれた)aの値をfirstaというオブジェクトに保存
for(i in 1:20){ #これまでのプログラムの外側に新しく作ったfor文。20回繰り返す。
a=firsta #繰り返しの最初に、aの値を初期値(firsta)に戻す
results=c()
for(j in 1:30){
counta=0
for(k in 1:20){
if ( runif(1) < a/20 ){
counta=counta+1
}
}
results=append(results, a/20)
a=counta
}
par(new=T) #複数のグラフを重ね合わせる
plot(results, type="l")
} #新しく作ったfor文の終わり。ここまで繰り返し。
}
あれれ?そうか。始点の軸が固定されていないから、ずれちゃってますね。plot()関数にはylimというオプションがあって、y軸の目盛りを0から1に固定するには、次のように書きます。
drift5=function(a){
firsta=a #関数に渡された(つまり()の中に書かれた)aの値をfirstaというオブジェクトに保存
for(i in 1:20){ #これまでのプログラムの外側に新しく作ったfor文。20回繰り返す。
a=firsta #繰り返しの最初に、aの値を初期値(firsta)に戻す
results=c()
for(j in 1:30){
counta=0
for(k in 1:20){
if ( runif(1) < a/20 ){
counta=counta+1
}
}
results=append(results, a/20)
a=counta
}
par(new=T) #複数のグラフを重ね合わせる
plot(results, type="l", ylim=c(0,1)) #y軸の目盛りを0から1に固定する
} #新しく作ったfor文の終わり。ここまで繰り返し。
}
いよいよ完成にちかづいてきました。図が重なって見にくくなったら、
>frame()
か
>plot.new()
で図を新しく書き直して下さい。
何回かグラフを描かしてみると、わりとすぐに固定してしまうことがわかりますね。じゃあ、もっと、集団サイズがもっと大きかったらどうなるか気になってくるでしょ?
どうすればよいか?プログラムの中で、集団サイズを20に指定しているところを100とかに変更してもいいのですが、どうせなら、関数に値を渡すときに、指定できれば、つまり、
drift(繰り返し数, 世代数, 集団サイズ, 対立遺伝子の数)
とか指定して実行できれば、好きな大きさの集団で、好きな数だけ、シミュレーションを繰り返せますよね。さっきのプログラムで、数値で指定してあったところを変数に置き換えるだけですから、そんなに難しくなさそうです。
では、やってみましょう
drift6=function(x, y, z, a){
plot.new() #ついでに、図を新しく書き直すという関数をここに追加しました
firsta=a
for(i in 1:x){ #上のプログラムでは20でしたが、ここでは、x回繰り返す。
a=firsta
results=c()
for(j in 1:y){ #上のプログラムでは30だったけど、ここではy世代繰り返す。
counta=0
for(k in 1:z){ #上のプログラムでは20だったけど、ここでは集団サイズはz。
if ( runif(1) < a/z ){ #上のプログラムでは20だったけど、ここでは集団サイズはz。
counta=counta+1
}
}
results=append(results, a/z) #上のプログラムでは20だったけど、ここでは集団サイズはz。
a=counta
}
par(new=T)
plot(results, type="l", ylim=c(0,1))
}
}
できちゃいました。 あんまり大きい数字を入れると計算にすごく時間がかかります。途中で終了したいときは、 ESC キーを押してください。
下のプログラムは遺伝的浮動をシミュレートするRのプログラムです。シミュレーションで観察する集団の数(num_repeats)、1集団あたり観察する世代数(num_generations)、集団サイズ(遺伝子数)(size_population)、0世代目における対立遺伝子aの数(num_a_allele)を与えて実行すれば、、ランダムに選ばれる遺伝子が、次世代の集団の遺伝子頻度にどのように影響するかを、シミュレートする集団の数だけグラフに(色つきで)表示することができます。下のプログラムを見て以下の問に答えなさい。
drift= function(num_repeats,num_generations,size_population, num_a_allele){
results=c()
a=num_a_allele
for(i in 1:【1】){
for(j in 1:【2】){
count_a=0
for(k in 1:size_population){
if ( runif(1) < a/【3】 ){
count_a=count_a+1
}
}
a=count_a
results=append(results, a/size_population)
}
a=num_a_allele
}
rmatrix=matrix(results, nrow=num_generations, ncol=num_repeats)
return(matplot(rmatrix, type="l"))
}
num_repeats, num_generations, size_population, num_a_allele
1. 実験の繰り返し数10回、1集団での観察世代数500世代、集団サイズ(遺伝子数)200, 初期状態での対立遺伝子aの数100 2. 実験の繰り返し数10回、1集団での観察世代数100世代、集団サイズ(遺伝子数)20, 初期状態での対立遺伝子aの数10実行するための命令文と、結果のグラフを、1, 2のいずれの場合についても、課題提出ページに貼り付けなさい(注:1番目のシミュレーションの実行には、数分かかるかもしれません)
drift6=function(x, y, z, a){
plot.new() #ついでに、図を新しく書き直すという関数をここに追加しました
firsta=a
for(i in 1:x){ #上のプログラムでは20でしたが、ここでは、x回繰り返す。
a=firsta
results=c()
results_p=c()
for(j in 1:y){
counta=0
count_p=0
count_p_type=0
for(k in 1:z){
if ( runif(1) < a/z ){
counta=counta+1
}
if (k%%2 != 0){ #jが奇数のとき
if ( runif(1) < a/z ){ #もし2つの遺伝子のうち最初のものがaならば
count_p=count_p+1 #count_pの値を1増やす
}
} else { #jが偶数のとき
if ( runif(1) < a/z ){ #もし2つの遺伝子のうち最初のものがaならば
count_p=count_p+1 #count_pの値を1増やす
}
if(count_p == 2){ #連続する奇数回・偶数回で合計したpの値が2ならば(つまり、aが2個だったら)
count_p_type=count_p_type+1 #count_p_typeの値を1増やす(aaとう表現型が1つあると数える)
}
count_p=0 #2個数え終わったら、count_pの値を初期化
}
}
results=append(results, a/z)
results_p=append(results_p, count_p_type/(z/2)) #results_pに集団内のaaの頻度(count_p_type/z/2)を入れる
count_p_type=0 #count_p_typeの値を初期化
a=counta
}
par(new=T)
plot(results, type="l", ylim=c(0,1))
par(new=T)
plot(results_p, type="l", ylim=c(0,1), col="blue") #aaの頻度を青線で表示する
}
}
drift6=function(x, y, z, a, s){ #選択係数sでaaが集団から排除される
plot.new()
firsta=a
for(i in 1:x){
a=firsta
results=c()
results_p=c()
for(j in 1:y){
counta=0
count_p=0
count_p_type=0
for(k in 1:z){
if (k%%2 != 0){ #jが奇数のとき
if ( runif(1) < a/z ){ #もし2つの遺伝子のうち最初のものがaならば
count_p=count_p+1 #count_pの値を1増やす
}
} else { #jが偶数のとき
if ( runif(1) < a/z ){ #もし2つの遺伝子のうち2番目のものがaならば
count_p=count_p+1 #count_pの値を1増やす
}
if(count_p == 2){ #連続する奇数回・偶数回で合計したpの値が2ならば(つまり、aが2個だったら)
if (runif(1) < s) { #遺伝子型がaaのとき乱数を一つとって、それが選択係数より小さければ
k=k-2 #jの値から2を引いて
count_p=0 #count_pを初期化し
next #強制的に次の繰り返し
} else {
count_p_type=count_p_type+1 #count_p_typeの値を1増やす(aaという表現型が1つあると数える)
}
}
counta=counta+count_p
count_p=0
}
}
results=append(results, a/z)
results_p=append(results_p, count_p_type/(z/2)) #results_pに集団内のaaの頻度(count_p_type/z/2)を入れる
count_p_type=0 #count_p_typeの値を初期化
a=counta
}
par(new=T)
plot(results, type="l", ylim=c(0,1))
par(new=T)
plot(results_p, type="l", ylim=c(0,1), col="blue") #aaの頻度を青線で表示する
}
}
wtime=function(x, y, z, a){
firsta=a
results_w=c()
for(i in 1:x){
a=firsta
results=c()
w_time=0
for(j in 1:y){
counta=0
for(k in 1:z){
if ( runif(1) < a/z ){
counta=counta+1
}
}
a=counta
if((w_time==0) && ((a==0) || (a==z))) { #もしw_timeが空で、aが0かzに固定しているとき、
w_time=j #w_timeにそのときに世代数jを入れる
}
}
results_w=append(results_w, w_time) #その集団における固定までの世代時間をresults_wに入れる
}
return(results_w)
}
drift6=function(x, y, z, a){
plot.new()
firsta=a
resultp_m=c()
for(i in 1:x){
a=firsta
results=c()
results_p=c()
for(j in 1:y){
counta=0
count_p=0
count_p_type=0
for(k in 1:z){
if ( runif(1) < a/z ){
counta=counta+1
}
}
results=append(results, a/z)
results_p=append(results_p, 2*(a/z)*(1-a/z)) #results_pに集団内のaaの頻度(count_p_type/z/2)を入れる
a=counta
}
resultp_m=append(resultp_m, results_p)
par(new=T)
plot(results, type="l", ylim=c(0,1), col="gray")
}
rmatrix=matrix(resultp_m, nrow=y, ncol=x)
hetero=c()
for(i in 1:y) {
hetero=append(hetero,mean(rmatrix[i,]))
}
par(new=T)
plot(hetero, type="l", ylim=c(0,1), col="blue")
par(new=T)
curve(0.5*(1-1/z)^x, xlim=c(0,y), ylim=c(0,1), col="red")
}