授業/H20/情報処理/11 のバックアップ(No.4)

• バックアップ一覧
• 差分 を表示
• 現在との差分 を表示
• ソース を表示
• 授業/H20/情報処理/11 へ行く。
  • 1 (2008-06-20 (金) 11:13:46)
  • 2 (2008-06-20 (金) 11:14:46)
  • 3 (2008-06-25 (水) 15:06:07)
  • 4 (2008-06-26 (木) 10:08:32)
  • 5 (2008-06-26 (木) 12:57:49)
  • 6 (2008-06-26 (木) 16:04:52)
  • 7 (2008-06-26 (木) 16:38:52)
  • 8 (2008-07-01 (火) 07:15:24)
  • 9 (2008-07-03 (木) 08:00:41)
  • 10 (2009-06-25 (木) 07:56:37)

---

このページは編集中です。完成予定は6月26日午後4時です。　Rを使ったプログラミング演習2：　シミュレーション †

第10回授業の獲得目標： †

• 1. プログラミングの基本：繰り返し・代入・条件分岐に習熟する
• 2. ユーザー定義関数を理解する
• 3. シミュレーションによる問題解決の方法を習得する

条件分岐 †

プログラミングの基本技の最後は条件分岐。if()を使って表現する。

i=4                       #iに4を代入
if(i==3){                 #iの値が3ならば
  print("三")            #   三 と表示する
} else {                  #iの値が3では無ければ
  print("三以外")   #   三以外と表示する
}

if命令の()の中の式を条件式といい、iの値を評価している。評価に使われるのは比較演算子というもので、

==　    等しければ
!=      等しく無ければ
>, >=   左辺が右辺より大きいなら、左辺が右辺以上ならば
<, <=   左辺が右辺より小さいなら、左辺が右辺以下ならば

ということを意味している

• r-tips.pdfで比較演算子を検索してみよう！

''比較演算子''である''=='' に対して、代入の時に使った ''='' は''代入演算子''といいう。

上のif命令では、次のような条件分岐が行われている。

if(i==3){
   print("三")
}
 ・もしiの値が３ならば、画面に三を表示。
 ・もしiの値が３で無いならば、何もしない
else {                  #iの値が3では無ければ
  print("三以外")   #   三以外と表示する
}

• else以下の処理が必要無いときは省略できる。また、1行に書くことも可能。

  i=3                       #iに3を代入
  if(i==3){ print("三") }   #iが3ならば三と表示

#演習：乱数を１つ発生させ、値が0.5以上なら「0.5以上」、0.5より小さいなら「0.5より小さい」と表示させる この演習では、乱数を発生させるrunif()という関数を使う。試しに

runif(5)

と入力してみよう。0から1までの乱数が5個表示されたはずだ。乱数はシミュレーションではよく使うので、もう少し慣れ親しんでおこう。 例えば、runif()を使って乱数を10個発生させ、ヒストグラムを書いてみよう。同じことを、100個、1000個、10000個、100000個についてもやってみよう。

hist(runif(10))

バラツキがだんだんと無くなってきたのがわかるだろうか。

#穴埋め式練習問題
if (runif(1) >= _ ) {   #条件式0.5以上ならば
  print("0.5以上")
} _ { 
  print("0.5より小さい")
}

繰り返しと条件分岐 †

　では、上の繰り返しと条件分岐を組み合わせて使ってみよう

練習問題：for命令を使って1から10までの数字を表示させなさい、5だけは"five"と英単語で表示させなさい

• ヒントを穴埋め式で示しておく。

  for(i in _:_){    #  10回繰り返し。iは1から10まで変化
    if(i == _) {    #iが5の場合
       print("five")       #fiveと表示
    } _ {       #それ以外の場合
       print(_)       #iの値を表示
    }
  }

関数の定義 †

「関数の定義」なんていうと難しそうだが、ようするに、先ほどまでに作ったプログラムに名前をつけて、いろいろと数値を変えて解析できるようにしようというものだ。こういうときに関数を定義する関数、'function()'を使う。 例えば、円の面積を計算する関数を作るなら、

 menseki=function(r){r*r*pai}

とすれば良い。これで自分独自の関数menseki()ができた。 では、実行してみよう。

menseki()

演習：1から入力した数値までの全てを横一列に表示させるプログラムを作りdisplayという名前の関数として定義する

display=function(a){       #関数定義の始まり
 kekka=c()                 #kekkaに空ベクトルを代入して初期化
 for(i in 1:a){              #a回（iの値を1からaまで変化させる間）繰り返し
   kekka=c(kekka,i)     #kekkaというベクトルにiを要素として代入
 }
 print(kekka)              #kekkaの内容を表示
}                          #関数定義の終わり

display(10)

↑を使って何回も実行してみると、結果がいろいろ変わるのがわかる。

演習上の関数の定義方法に従って、入力した数までの合計値を計算するsumupという名前の関数を作成する。下の囲みの中の_の部分（１文字に対応するとは限らない）を埋めて、プログラムを完成しなさい。

 sumup = ______       #関数sumpuを定義
   kotae = _          #kotaeを初期化
   _ (i in ___){      #1からaまで繰り返し
     kotae = _____    #kotaeにiの値を足したものとkotaeに代入
   }                  #繰り返し終了
  _____               #kotaeを表示
  }                   #関数定義の終了

繰り返し・代入・条件分岐のおさらい †

次のそれぞれのプログラムの＿部分に何を入れるべきかを選択肢から選びなさい。また、Rを使って実行してみましょう。

繰り返し †

for(i in 1:__){    #{と}の間を10回繰り返す。i の値は毎回1ずつ増える
  print(i)
}

選択肢： a) 1    b)  5     c) 

代入 †

goukei=0           #goukeiという変数に初期値0を代入
for(i in 1:10) {   
  goukei=_____+i  #goukeiに前回までのgoukeiの値にiの値を足したもの代入
} 
print(goukei)

選択肢： a) i    b)  goukei   c) 

条件分岐 †

goukei=0           #goukeiという変数に初期値0を代入
 for(i in 1:10) {
   if(i %% 2 __ 0) { # %% は割り算をした余りを返す演算子。3 %% 2 の計算結果は 1 になる
     goukei=goukei+i # if文の内容は：　「もし i を 2 で割った余りが 0 ならば、{}内を実行
   }               #それ以外は何もしない
 }              #for 文のカッコ閉じるに注意
 print(goukei)

選択肢： a) =    b)  ==     c) <=

授業で使ったRの基本関数 †

授業で使うR関数一覧 †

演算子 †

定数（Rの基本システムで決まっている値):　次の５つ †

> LETTERS
  [1] "A" "B" "C" "D" "E" "F" "G" "H" "I" "J" "K" "L" "M" "N" "O" "P" "Q" "R" "S" "T" "U"
 [22] "V" "W" "X" "Y" "Z"
> letters
 [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t" "u"
 [22] "v" "w" "x" "y" "z"
> month.abb
  [1] "Jan" "Feb" "Mar" "Apr" "May" "Jun" "Jul" "Aug" "Sep" "Oct" "Nov" "Dec"
> month.name
  [1] "January"   "February"  "March"     "April"     "May"       "June"      "July"     
  [8] "August"    "September" "October"   "November"  "December" 
> pi
 [1] 3.141593

関数 †

Rを用いたシミュレーション †

これまでに学んだ繰り返し・代入・条件分岐の３つの命令それぞれは単純だが、組み合わせれば、かなり複雑なこと表現できる。そこで、今回は、これらの命令を組み合わせて、Rを用いたシミュレーションに挑戦してみよう。

円周率(π）をモンテカルロ法で求める †

simpai=function(x){
	kaisu=0;  #回数の初期値を0にする
	for (i in 1:x) {
		point=runif(2)
		distant=sqrt(point[1]^2+point[2]^2)
		if(distant<1){
			kaisu=kaisu+1
		}
	}
	answer=4*kaisu/x
	print(answer)
}
> simpai(10)
[1] 2.8
> simpai(100)
[1] 3.16
> simpai(1000)
[1] 3.156
> simpai(10000)
[1] 3.1624
> simpai(100000)
[1] 3.15652
> simpai(1000000)
[1] 3.13994
> simpai(10000000)
[1] 3.140556

せっかくだから、点をうつところを図で表現してみよう †

simpai=function(x){
	kaisu=0;  #回数の初期値を0にする
	for (i in 1:x) {
		point=runif(2)
               par(new=T)    #複数のグラフを重ね合わせる
               plot(point[1], point[2], ylim=c(0,1), xlim=c(0,1))  #0-1の範囲で乱数の値をプロット
		distant=sqrt(point[1]^2+point[2]^2)
		if(distant<1){
			kaisu=kaisu+1
		}
	}
	answer=4*kaisu/x
	print(answer)
}

袋の中から赤玉・青玉を取り出す実験のシミュレーション †

赤玉と青玉が同じ数だけたくさん入った筒から、20個の玉を取り出して、その中に含まれる赤玉の割合に従って筒に含まれる赤玉の個数を変え、また20個取り出す。。。こういう操作を何度も繰り返すというモデルで、何度も実験すると、袋の中の玉の割合がどのように変化するかをシミュレーションで示してみよう。

「赤玉と青玉の同じ数入っている筒から無作為に20個の玉を取り出したら、赤玉が7個入っていた」
  -----------------------------------------------------
上でやった操作には、「20個取り出して赤玉かどうか判断する」というところに「繰り返し」が含まれている。
「繰り返し」がはっきりと分かるように説明すると、
 1. 筒からボールを一つ取り出す
 2. そのボールが赤玉だったら数える（１つ目だったら「一つ」、２つめは「２つ」..)。青玉だったら数えない
 3.  1 と 2 の操作を20回繰り返す

この部分を大雑把でいいので、プログラミングしてみる。繰り返しはfor文で表現できる

 カウンタの値は最初は0にしておく
 for ( 20回繰り返す  ) {
   if (取り出したのが赤玉だったら) {
     カウンタの値を１増やす
   }
 }

カウンタのところは代入文で表現できる。for文も、Rで実行できる形式に直す

 カウンタ = 
 for ( i in 1:20 ) {
   if (取り出したのが赤玉だったら) {
     カウンタ = カウンタ + 
   }
 }

「もし、取り出したのが赤玉だったら」というif文をどうプログラミングすれば良いかが、今回のシミュレーションの最重要ポイントだろう。この部分は乱数を使って表現できる。

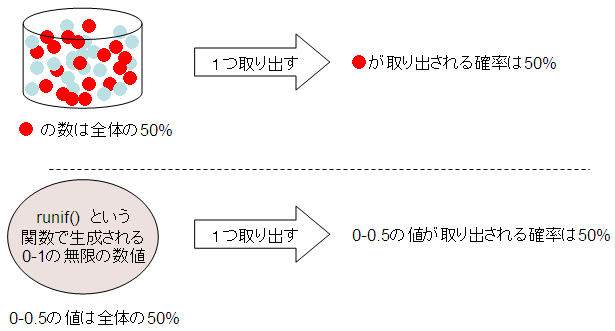
つまり、0-1の範囲の乱数を１つ発生させ、それが0.5よりも小さい値だったら、赤玉が取り出されたとみなせばいい。 乱数を１つ発生させるには runif(1) を使う。

 カウンタ = 
 for ( i in 1:20 ) {
   if (runif(1) < 0.5 ) {
     カウンタ = カウンタ + 
   }
 }

これで20個取り出したうちの赤玉の個数を数えるという部分は完成です

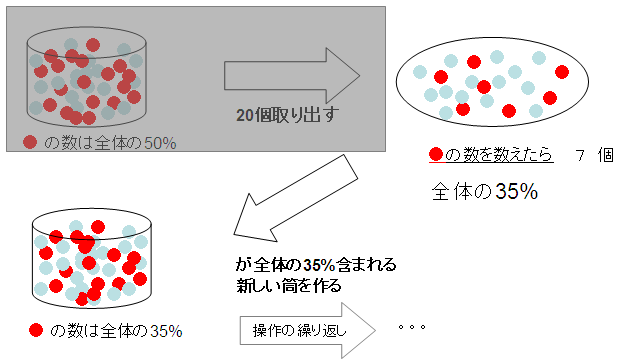
上の図で、最初の矢印の部分の操作を行い、筒から取り出した赤玉の数を数えるシミュレーションのプログラミングは終わりました。次に、取り出した赤玉の割合になるように筒の中の赤玉の数を変更して、同様の操作を100回繰り返すという部分のプログラミングを考えます。繰り返しが含まれているのでfor文を使って大雑把に書くと、

 for ( j in 1:100 ) {   #さっきiという変数を使ったので、ここではjを使う
   ※20個取り出して赤玉の数を数える
 }

たったこれだけです。上で作った赤玉の数を数えるプログラムを※のところに入れてみると

 for ( j in 1:100 ) {   #さっきiという変数を使ったので、ここではjを使う
   カウンタ = 
   for ( i in 1:20 ) {
     if (runif(1) < 0.5 ) {
       カウンタ = カウンタ + 
     }
   }
 }

ん？？これでは上の図の例で、20個取り出した中に含まれていた赤玉の数の割合に、筒の中の赤玉の割合を変更したことが反映されていませんね。取り出した赤玉の数は、内側のfor文が終わった後に、カウンタの値を20で割ることで求められますから、「赤玉の割合」という変数を一つ作って、毎回、新しい値をこの変数に入れるようにしましょう。

 赤玉の割合=0.5         #初期値は0.
 for ( j in 1:100 ) {   #さっきiという変数を使ったので、ここではjを使う
   カウンタ = 
   for ( i in 1:20 ) {
     if (runif(1) < 赤玉の割合 ) {
       カウンタ = カウンタ + 
     }
   }
   赤玉の割合 = カウンタ/20  #20個の中の赤玉の割合を算出
 }

あとは結果をプリントする文を入れれば完成です。何回目に固定したかが分かるように、j の値も一緒にプリントするようにしましょう。

 赤玉の割合=0.5         #初期値は0.
 for ( j in 1:100 ) {   #さっきiという変数を使ったので、ここではjを使う
   カウンタ = 
   for ( i in 1:20 ) {
     if (runif(1) < 赤玉の割合 ) {
       カウンタ = カウンタ + 
     }
   }
   赤玉の割合 = カウンタ/20  #20個の中の赤玉の割合を算出
   結果=c(j, 赤玉の割合)
   print(結果)
 }

最後に †

昨年、同様の授業を行ったところ、受講生から次のような質問がありました。

「こういうシミュレーションのプログラミングって、これから生物学を学ぶのに、どのくらい必要なんですか？」

これまでプログラミングなどしたことの無い人にとって、とても素朴な疑問だろうと思います。そこで、次のように答えておきました。

画一的な答えは難しいです。シミュレーションそのものが直接必要になるような分野もあれば、そうでない分野もあります。
ただ、私は、プログラミングは、生物学における発展的な情報処理をする上での基本技だと考えています。
千葉大の研究室に限って言えば、プログラミング技術が無いと卒業研究が終わらないというところは
現時点では（たぶん）無いでしょう。但し、プログラミングができると、卒業研究や修士の研究でより
進んだことができたり、理解が深まったり、研究が楽になるようなところはいくつもあります。
将来、数理生物学、理論集団遺伝学、進化生態学、バイオインフォマティクスを志す人には、
敢えて、不可欠な技術だと言っておきます。

第11回授業の課題 †

課題2: 課題 †

下のプログラムは遺伝的浮動をシミュレートするRのプログラムです。このシミュレーションで観察する集団の数(num_repeats)、１集団あたり観察する世代数(num_generations)、集団サイズ（遺伝子数）(size_population)、０世代目における対立遺伝子aの数(num_a_allele)を与えて実行すれば、、ランダムに選ばれる遺伝子が、次世代の集団の遺伝子頻度にどのように影響するかを、シミュレートする集団数（観察集団数）の数だけ色つきの折れ線グラフで表示することができます。下のプログラムを見て以下の問に答えなさい。

drift= function(num_repeats,num_generations,size_population, num_a_allele){
	 results=c()
        a=num_a_
	 for(i in 1:【1】){
		  for(j in 1:【2】){
		      count_a=
		       for(k in 1:size_population){
			    if ( runif(1) < a/【3】 ){
			     count_a=count_a+
			    }
		       }
		       a=count_
		       results=append(results, a/size_population)
		  }
		  a=num_a_
	 }
	 rmatrix=matrix(results, nrow=num_generations, ncol=num_repeats)
	 return(matplot(rmatrix, type="l"))
}

• 問1: プログラム中【1】〜【3】に入る変数名を、下のリストから選んで答えなさい

  num_repeats, num_generations, size_population, num_a_

  • それぞれの変数は次のような意味を持っています
    • num_repeats : シミュレーションを行う集団数（１つの集団についてある世代数だけ観察するという実験を、何回（何個の集団について）おこなうか）、すなわち観察集団数。何本の折れ線グラフを表示させるかはこの値で決まる。
    • num_generations : 1つの集団について何世代続けて観察するか。x軸の長さになります。
    • size_population : 集団のサイズ、つまり、１つの集団に含まれる遺伝子の総数
    • num_a_allele : aアリルの数（つまり、この値をnum_populationで割ったものが、0世代目でのaアリルの遺伝子頻度になる）
• 問2: 上のプログラム中、【1】〜【3】を問1で答えた変数で置き換え、次の２つの場合を実行しなさい。

  1. 実験の繰り返し数10回、1集団での観察世代数500世代、集団サイズ（遺伝子数）200, 初期状態での対立遺伝子ａの数
  2. 実験の繰り返し数10回、1集団での観察世代数100世代、集団サイズ（遺伝子数）20, 初期状態での対立遺伝子ａの数
  いずれの場合についても、できたグラフをWinShotで切り取って、課題提出ページに貼り付けなさい（注：1番目のシミュ
  レーションの実行には、数分かかるかもしれません）（注：あまり大きい図（画面全面に広がる図とか）にはしないでく
  ださい）

• 問3: 上の２つのグラフを比較して分かることを述べなさい。

[ トップ ]   [ 新規 | 一覧 | 単語検索 | 最終更新 | ヘルプ ]

Site admin: Tadashi Kajita

PukiWiki 1.4.7 Copyright © 2001-2006 PukiWiki Developers Team. License is GPL.
Based on "PukiWiki" 1.3 by yu-ji. Powered by PHP 5.3.29. HTML convert time: 0.035 sec.