![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[worried]](image/face/worried.png) †
†![[smile]](image/face/smile.png) †
†次のそれぞれのプログラムの_部分に何を入れるべきかを選択肢から選びなさい。また、Rを使って実行してみましょう。
for(i in 1:__){ #{と}の間を10回繰り返す。i の値は毎回1ずつ増える
print(i)
}
選択肢: a) 1 b) 5 c) 10goukei=0 #goukeiという変数に初期値0を代入
for(i in 1:10) {
goukei=_____+i #goukeiに前回までのgoukeiの値にiの値を足したもの代入
}
print(goukei)
選択肢: a) i b) goukei c) printgoukei=0 #goukeiという変数に初期値0を代入
for(i in 1:10) {
if(i %% 2 __ 0) { # %% は割り算をした余りを返す演算子。3 %% 2 の計算結果は 1 になる
goukei=goukei+i # if文の内容は: 「もし i を 2 で割った余りが 0 ならば、{}内を実行
} #それ以外は何もしない
} #for 文のカッコ閉じるに注意
print(goukei)
選択肢: a) = b) == c) <=![[smile]](image/face/smile.png) †
†「ユーザー定義関数」なんていうと難しそうだが、ようするに、先ほどまでに作ったプログラムに名前をつけて、いろいろと数値を変えて解析できるようにしようというものだ。こういうときに関数を定義する関数、function()を使う。 例えば、円の面積を計算する関数を作るなら、
menseki=function(r){r*r*pi}
とすれば良い。これで自分独自の関数menseki()ができた。 では、実行してみよう。
menseki(10) #好きな数字を入れて円の面積を計算
演習 1: 1から入力した数値までの全てを横一列に表示させるプログラムを作りdisplayという名前の関数として定義する
display=function(a){ #関数定義の始まり
kekka=c() #kekkaに空ベクトルを代入して初期化
for(i in 1:a){ #a回(iの値を1からaまで変化させる間)繰り返し
kekka=c(kekka,i) #kekkaというベクトルにiを要素として代入
}
print(kekka) #kekkaの内容を表示
} #関数定義の終わり
display(10)
↑を使って何回も実行してみると、結果がいろいろ変わるのがわかる。
演習2: 上の関数の定義方法に従って、入力した数までの合計値を計算するsumupという名前の関数を作成する。下の囲みの中の_の部分(1文字に対応するとは限らない)を埋めて、プログラムを完成しなさい。
sumup = ______ #関数sumpuを定義
kotae = _ #kotaeを初期化
_ (i in ___){ #1からaまで繰り返し
kotae = _____ #kotaeにiの値を足したものとkotaeに代入
} #繰り返し終了
_____ #kotaeを表示
} #関数定義の終了
![[smile]](image/face/smile.png) †
†これまでに学んだ繰り返し・代入・条件分岐の3つの命令それぞれは単純だが、組み合わせれば、かなり複雑なこと表現できる。そこで、今回は、これらの命令を組み合わせて、Rを用いたシミュレーションに挑戦してみよう。
シミュレーションという言葉は「株式シミュレーション」とか「シミュレーションゲーム」とかで聞いたことがあるだろう。日本語にすると、「模擬実験」で、自分では実行が難しい繰り返し実験を、コンピュータに計算させることで行うものだ。コンピュータは単純な繰り返し計算は得意なので、砂粒をばらまいて、ある図形の中に入った数を数えるなんていう作業を、10万回でも、100万回でも繰り返すことができる。
シミュレーションをうまく使えば、たとえ数学的に解くのが難しい問題についても、近い答えを求めることができる。また、ある現象について作成したモデルを用い、パラメーターの変化がどのような状態の変化をもたらすかを予測することができるため、進化生物学や生態学でもよく使われる。
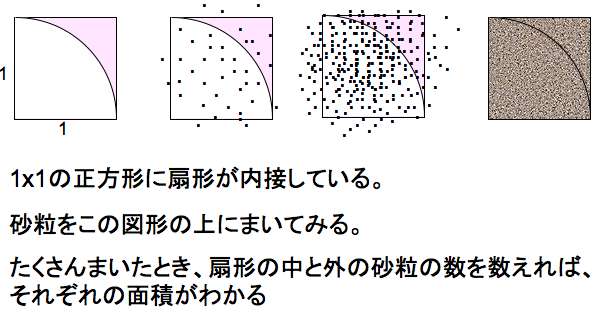
左に1辺の長さが1の正方形と、それに内接する扇形がある。このとき、
正方形の面積は 1 扇形の面積は π/4
この図形の上に、砂粒をばらまいてみる。 砂粒が図形の上にランダムに散らばるとすると、砂粒をすごく沢山まいて数を数えれば、
正方形の中の砂粒の数(n) : 扇形の中砂粒の数(m) = 正方形の面積 :扇形の面積 = 1 : π/4
になると考えられる。つまり
n : m = 1 : π/4 だから、 π = 4m/n
もしあなたが、砂粒をたくさんランダムにまいて、正方形の中の砂粒と扇形の中の砂粒の数を数えることができれば、πの値がわかるということになる。自分で実際に実験することを想像すると、恐ろしく大変だが、そういう面倒な実験はコンピュータにやらせてしまえばいい!
さて、砂粒を沢山まいて、それが円の中か外かを判定する実験を、コンピュータにやらせるにはどうすればよいだろうか。
まず、点(砂粒)を大量に発生させる必要がある。さて、どうすればいいだろうか?
もうお分かりのように、「繰り返し」命令(for文)を使う。
#とりあえず、1,000つぶの砂をまくことをfor文で表現する
for (i in 1:1000){
<砂を1粒図形の上にまく>
}
次に、砂を1粒図形の上にまいて、それが扇形の中か外かを判定することを考える。
砂を1粒まくことは、無作為に(ランダムに)図形の上に点を打つことと同じことだ。「ランダム」というと、我々はすでに乱数を発生させる方法をしっている。図形の上に1つの点を打つということは、2つの乱数を発生させることで表現できるだろう。
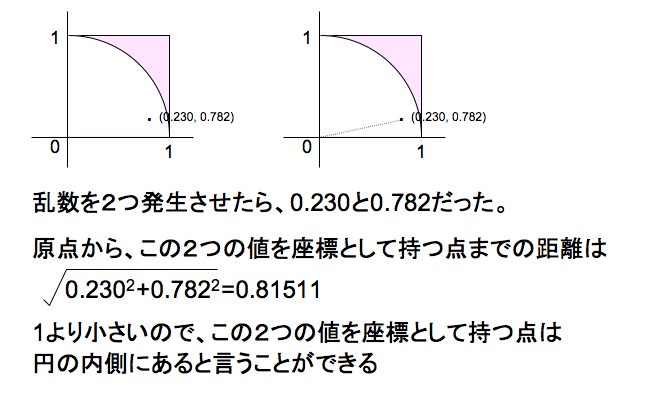
例えば、0-1の範囲の乱数を2つ発生させたら、 (0.230 , 0.782) という2つの数字が得られたとする。この2つの数字が座標上の点を表していると考えると、上の図のようになる。
原点からこの点までの距離が1より小さいとき、この点は扇形の中に入っているということができる。
Rでは平方根を表すとき、 sqrt()という関数を使うので、この例では、
sqrt(0.230^2+0.782^2) < 1
となり、ランダムに発生させた(図形の上に偶然落ちた)1つの点は、扇形の中だったということになる。
実際に2つの乱数を発生させて、それを、pointというオブジェクトに代入するには、次のようにする。
point=runif(2) #この命令で、0-1の範囲の乱数を2つ発生させ、pointというベクトルに入れる
このとき、pointに入ったそれぞれの値を指定するには、
point[1] point[2]
のようにカギ括弧[]を使う。
例: []の使い方を、試してみよう
> x=runif(2)
> x
> x[1]
> x[2]
砂粒(点)が扇形の中かどうかを判断するにはどうすれば良いか?これは条件分岐で表現できる。つまり、runif(2)で発生させた2つの数値のそれぞれを2乗して足しあわせたものの平方根が1より小さいか否かを判断する。
#扇形の中かどうかを判断する条件文
distant=sqrt(point[1]^2+point[2]^2) #発生させた2つの乱数の2乗の和の平方根
if(distant<1){ #原点からの距離が1より小さければ扇形の中
<個数を数える>
}
では、個数を数えるにはどうすればよいか?ここでは代入文を使う
#個数を数える部分
kaisu=0 #回数の初期値を0にする
if(distant<1){ #原点からの距離が1より小さければ扇形の中
kaisu = kaisu + 1 #条件にあったとき、kaisuの値を1増やす
}
以上のように、これまでに学習した、繰り返し、条件分岐、代入で、図形の上に砂粒を1000個まく実験が表現できた。πの値は砂粒の個数を4倍して、全体の個数で割ったものだから、以上をまとめると次のようになる。
kaisu=0; #個数の初期値を0にする
for (i in 1:1000) {
point=runif(2)
distant=sqrt(point[1]^2+point[2]^2)
if(distant<1){
kaisu=kaisu+1
}
}
answer=4*kaisu/1000
print(answer)
さらに、functionを使って、好きな回数繰り返せる関数を定義してみよう
simpai=function(x){
kaisu=0; #個数の初期値を0にする
for (i in 1:x) {
point=runif(2)
distant=sqrt(point[1]^2+point[2]^2)
if(distant<1){
kaisu=kaisu+1
}
}
answer=4*kaisu/x
print(answer)
}
> simpai(10)
[1] 2.8
> simpai(100)
[1] 3.16
> simpai(1000)
[1] 3.156
> simpai(10000)
[1] 3.1624
> simpai(100000)
[1] 3.15652
> simpai(1000000) #ここから先は時間がかかるので、授業中はやらない方がいい
[1] 3.13994
> simpai(10000000) #ここから先は時間がかかるので、授業中はやらない方がいい
[1] 3.140556
simpai=function(x){
kaisu=0; #回数の初期値を0にする
for (i in 1:x) {
point=runif(2)
par(new=T) #複数のグラフを重ね合わせる
plot(point[1], point[2], ylim=c(0,1), xlim=c(0,1)) #0-1の範囲で乱数の値をプロット
distant=sqrt(point[1]^2+point[2]^2)
if(distant<1){
kaisu=kaisu+1
}
}
answer=4*kaisu/x
print(answer)
}
simpai=function(x){
kaisu=0; #個数の初期値を0にする
for (_ in 1:_) {
for (_ in 1:_) {
point=c(___,___)
distant=sqrt(point[1]^2+point[2]^2)
if(distant<1){
kaisu=kaisu+1
}
}
}
answer=4*kaisu/x^2
print(answer)
}
![[smile]](image/face/smile.png) †
†遺伝的浮動とは、
大きさの決まった集団で起きる、配偶子のランダムサンプリングによる遺伝子頻度の変動
のことだ。例えば、集団中の2つの対立遺伝子を、青玉と赤玉で表すと、袋(配偶子の集団: 配偶子の数はものすごく多いが、青と赤はそれぞれ50%)から取り出される青玉・赤玉の割合(集団中の遺伝子頻度)には、下の図に示したような変動が生じる(下の例で、青玉の遺伝子頻度は、0.8, 0.7, 1.0, と変動している)。もし、袋から取り出されたのが青玉ばっかり(あるいは、赤玉ばっかり)だと、それ以降、何度繰り返しても変化は生じない(これを、「集団は__に固定した」という)。
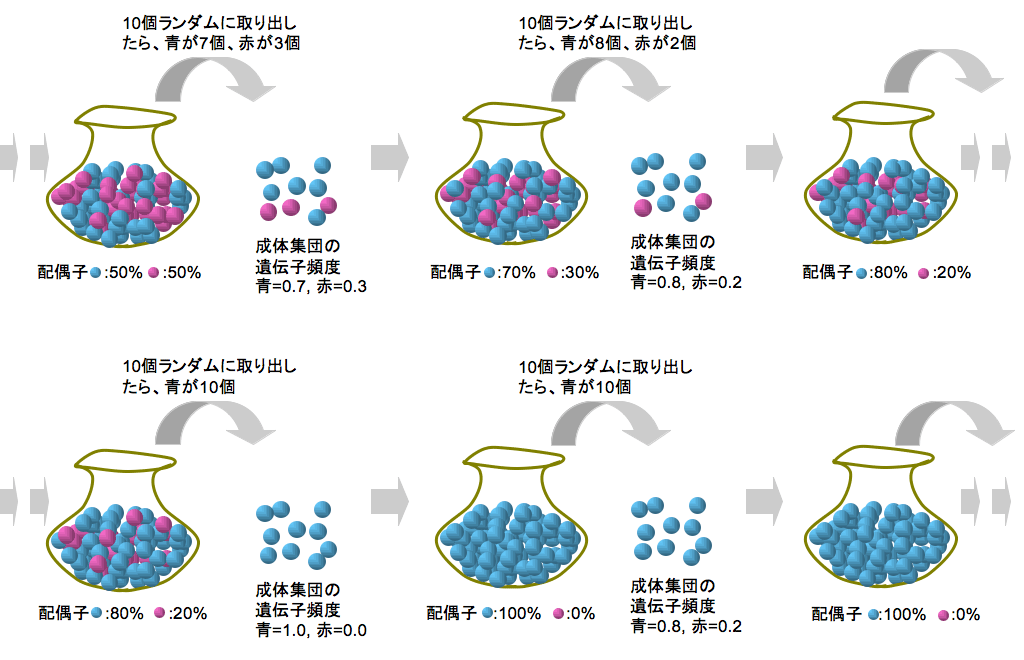
それでは、赤玉と青玉が同じ数だけたくさん入った袋から、10個の玉を取り出して、その中に含まれる青玉の割合に従って袋に含まれる青玉配偶子の個数を変え、また10個取り出す。。。こういう操作を何度も繰り返すというモデルで何度も実験を繰り返すと、袋の中の玉の割合がどのように変化するかをグラフで示してみよう。
質問: この実験を何度も繰り返しておこなうとき、 袋の中の玉が赤か白かどちらか1色になってしまうのは、何回目だろうか? 初期値: 袋の中の青玉と赤玉の数は同数 袋から取り出すのは10個
もう皆さんは"繰り返し、代入、条件分岐''というプログラミングの基本技を修得しているので、今問題にしている実験を、この3つのワザを使ってどのように表現するかが、最も重要なポイントだ。
「赤玉と青玉の同じ数入っている袋から無作為に10個の玉を取り出したら、青玉が7個入っていた」 ----------------------------------------------------- 上でやった操作には、「10個取り出して青玉かどうか判断する」というところに「繰り返し」が含まれている。 「繰り返し」がはっきりと分かるように説明すると、 1. 袋からボールを一つ取り出す 2. そのボールが青玉だったら数える(1つ目だったら「一つ」、2つめは「2つ」..)。青玉だったら数えない 3. 1 と 2 の操作を10回繰り返すこの部分を大雑把でいいので、プログラミングしてみる。繰り返しはfor文で表現できる
カウンタの値は最初は0にしておく
for ( 10回繰り返す ) {
if (取り出したのが青玉だったら) {
カウンタの値を1増やす
}
}
カウンタのところは代入文で表現できる。for文も、Rで実行できる形式に直す
カウンタ = 0
for ( i in 1:10 ) {
if (取り出したのが青玉だったら) {
カウンタ = カウンタ + 1
}
}0-1の範囲の乱数を1つ発生させ、それが0.5よりも小さい値だったら、 青玉が取り出されたとみなすそこで、乱数を1つ発生させるには runif(1) を使い、上のプログラム「取り出したのが青玉だったら」の部分を書き換える
カウンタ = 0
for ( i in 1:10 ) {
if (runif(1) < 0.5 ) {
カウンタ = カウンタ + 1
}
}
print(カウンタ) #この命令で'カウンタ'という変数の内容を表示
これで10個取り出したうちの青玉の個数を数えるという部分は完成!&ref(): File not found: "#11_2.jpg" at page "授業/H21/情報処理/11";
上の図で、最初の矢印の部分の操作を行い、袋から取り出した青玉の数を数えるシミュレーションのプログラミングは終わった。次に、取り出した青玉の割合になるように袋の中の青玉配偶子の割合を変更して、同様の操作を100回繰り返すという部分のプログラミングを考える。
繰り返しが含まれているのでfor文を使って書けることは分かるだろう
for ( j in 1:100 ) { #さっきiという変数を使ったので、ここではjを使う
※10個取り出して青玉の数を数える
}
たったこれだけ。
上で作った青玉の数を数えるプログラムを※のところに入れてみると
for ( j in 1:100 ) { #さっきiという変数を使ったので、ここではjを使う
カウンタ = 0
for ( i in 1:10 ) {
if (runif(1) < 0.5 ) {
カウンタ = カウンタ + 1
}
}
print(カウンタ) #カウンタの内容を表示
}
実際に走らせてみると、、、、???ん?何度やっても0や10に固定しない。 青玉の頻度=0.5 #初期値は0.5
for ( j in 1:100 ) { #さっきiという変数を使ったので、ここではjを使う
カウンタ = 0
for ( i in 1:10 ) {
if (runif(1) < 青玉の頻度 ) {
カウンタ = カウンタ + 1
}
}
青玉の頻度 = カウンタ/10 #10個の中の青玉の割合を算出
print(カウンタ) #この命令で'カウンタ'という変数の内容を表示
}
これを実行すると、何回目かには0か1に固定することができる。 青玉の割合=0.5 #初期値は0.5
for ( j in 1:100 ) { #さっきiという変数を使ったので、ここではjを使う
カウンタ = 0
for ( i in 1:10 ) {
if (runif(1) < 青玉の割合 ) {
カウンタ = カウンタ + 1
}
}
青玉の割合 = カウンタ/10 #10個の中の青玉の割合を算出
結果=c(j, 青玉の割合)
print(結果)
}(0.65, 0.7, 0.75, 0.85, ....)という形式にしておく必要がある。そこで、最初に空ベクトルを1つ作っておき、カウンタの値をベクトルに保存し、最後にplot()でグラフにする。
結果=c() #空ベクトル
青玉の頻度=0.5 #初期値は0.5
for ( j in 1:100 ) { #さっきiという変数を使ったので、ここではjを使う
カウンタ = 0
for ( i in 1:10 ) {
if (runif(1) < 青玉の頻度 ) {
カウンタ = カウンタ + 1
}
}
青玉の頻度 = カウンタ/10 #10個の中の青玉の割合を算出
結果=c(結果,青玉の頻度) #青玉の頻度を結果というベクトルに追加
}
plot(結果) #最後に結果をグラフにプロットplot(結果, type="l")に置き換えるだけです。
y軸の目盛りを0から1に固定するには、plot()関数のylimというオプションを使う
結果=c() #空ベクトル
青玉の頻度=0.5 #初期値は0.5
for ( j in 1:100 ) { #さっきiという変数を使ったので、ここではjを使う
カウンタ = 0
for ( i in 1:10 ) {
if (runif(1) < 青玉の頻度 ) {
カウンタ = カウンタ + 1
}
}
青玉の頻度 = カウンタ/10 #10個の中の青玉の割合を算出
結果=c(結果,青玉の頻度) #青玉の頻度を結果というベクトルに追加
}
plot(結果, type="l", ____=c(0,1)) #★★ylimを使ってy軸の目盛りを0から1に固定する実行してみると、うまくいってるようだが、1回ずつ、グラフが変わってしまう。グラフを重ねて描くには、par(new=T) というコマンドをplot()の前に使う。もしいくつもグラフを重ねて描いて、グラフが汚くなってしまったら、
frame() か plot.new()
というコマンドを使ってグラフをクリアする。
結果=c() #空ベクトル
青玉の頻度=0.5 #初期値は0.5
for ( j in 1:100 ) { #さっきiという変数を使ったので、ここではjを使う
カウンタ = 0
for ( i in 1:10 ) {
if (runif(1) < 青玉の頻度 ) {
カウンタ = カウンタ + 1
}
}
青玉の頻度 = カウンタ/10 #10個の中の青玉の割合を算出
結果=c(結果,青玉の頻度) #青玉の頻度を結果というベクトルに追加
}
par(new=T)
plot(結果, type="l", ____=c(0,1)) #★★ylimを使ってy軸の目盛りを0から1に固定する
なんども実行してみると、グラフがどんどん重なって書き換わるのが分かる。1回のキー操作が、1回の実験に相当している。キー操作で書き換えるのは、面倒なので、最初から実験回数を入力して、その回数だけ自動的に繰り返すような関数を作ってみよう。
注意: 1回の実験が終わる度に、青玉の頻度を0.5に、結果のベクトルを空にリセットすることを忘れないこと
drift=function(x){
frame() #グラフをクリアする
青玉の初期値=0.5 #初期値は0.5
for(k in 1:x){ #関数に与えた値の数だけ実験を繰り返す
青玉の頻度=青玉の初期値
結果=c() #空ベクトル
for ( j in 1:100 ) { #さっきiという変数を使ったので、ここではjを使う
カウンタ = 0
for ( i in 1:10 ) {
if (runif(1) < 青玉の頻度 ) {
カウンタ = カウンタ + 1
}
}
青玉の頻度 = カウンタ/10 #10個の中の青玉の割合を算出
結果=c(結果,青玉の頻度) #青玉の頻度を結果というベクトルに追加
}
par(new=T)
plot(結果, type="l", ylim=c(0,1)) #★★ylimを使ってy軸の目盛りを0から1に固定する
}
}
上のシミュレーションは集団の遺伝子の数が10の場合だけのシミュレーションだった。そこで、遺伝子の数(集団サイズ)、遺伝子頻度の初期値、繰り返し世代数、繰り返し実験数の全てを指定できるような関数を作ってみよう。複数の引数は、function()の中でカンマを使って指定できる
drift=function(実験回数, 初期頻度,集団サイズ,世代数){
frame() #グラフをクリアする
for(k in 1:実験回数){ #関数に与えた実験回数だけ実験を繰り返す
青玉の頻度=初期頻度
結果=c() #空ベクトル
for ( j in 1:世代数 ) { #さっきiという変数を使ったので、ここではjを使う
カウンタ = 0
for ( i in 1:集団サイズ ) {
if (runif(1) < 青玉の頻度 ) {
カウンタ = カウンタ + 1
}
}
青玉の頻度 = カウンタ/集団サイズ #集団サイズ個の中の青玉の割合を算出
結果=c(結果,青玉の頻度) #青玉の頻度を結果というベクトルに追加
}
par(new=T)
plot(結果, type="l", ylim=c(0,1)) #★★ylimを使ってy軸の目盛りを0から1に固定する
}
}
./11
*第11回授業・基本課題 **氏名: **課題への回答 -今日の授業の進み方は?(はやい、丁度いい、おそい) --回答: -今日の授業の難しさはどう感じましたか(簡単 丁度いい 難しい): --回答: -難しいと答えた人は、特にどの点が難しかったですか?: --回答: -今日の授業は(分かった 半分ぐらいは分かった 分からなかった): --回答: -分からないと答えた人は、特にどの点が分からなかったですか?: --回答: -今日の講義で分からなかった用語があったら挙げてください: --回答: -授業に関する要望・質問があったらなんでもどうぞ: --回答: -課題2の答え --問1 --【1】: --【2】: --【3】: --【4】: --問2: ---追加する命令と追加する場所: ---得られたヒストグラム: -課題3の答え --問1 --【1】: --【2】: --【3】: --問2-1: --問2-2: --問3:
下のプログラムは、正常なコイン(表、裏の出る確率はそれぞれ0.5)を100回投げて、表の出た回数を記録するという実験を、1000回繰り返すシミュレーションのプログラムです。
omote=0 #表の出る回数を初期化
kekka=c()
for(i in 1:【1】){
for (i in 1:【2】){
if(runif(1)<【3】){
omote=【4】+1
}
}
kekka=c(kekka,omote)
omote=0 #表の出る回数を初期化
}
print(kekka)
下のプログラムは遺伝的浮動をシミュレートするRのプログラムです。このシミュレーションで観察する集団の数(num_repeats)、1集団あたり観察する世代数(num_generations)、集団サイズ(遺伝子数)(size_population)、0世代目における対立遺伝子aの数(num_a_allele)を与えて実行すれば、、ランダムに選ばれる遺伝子が、次世代の集団の遺伝子頻度にどのように影響するかを、シミュレートする集団数(観察集団数)の数だけ色つきの折れ線グラフで表示することができます。下のプログラムを見て以下の問に答えなさい。
drift= function(num_repeats,num_generations,size_population, num_a_allele){
results=c()
a=num_a_allele
for(i in 1:【1】){
for(j in 1:【2】){
count_a=0
for(k in 1:size_population){
if ( runif(1) < a/【3】 ){
count_a=count_a+1
}
}
a=count_a
results=append(results, a/size_population)
}
a=num_a_allele
}
rmatrix=matrix(results, nrow=num_generations, ncol=num_repeats)
return(matplot(rmatrix, type="l"))
}
num_repeats, num_generations, size_population, num_a_allele
1. 実験の繰り返し数10回、1集団での観察世代数500世代、集団サイズ(遺伝子数)200, 初期状態での対立遺伝子aの数100 2. 実験の繰り返し数10回、1集団での観察世代数100世代、集団サイズ(遺伝子数)20, 初期状態での対立遺伝子aの数10 いずれの場合についても、できたグラフをWinShotで切り取って、課題提出ページに貼り付けなさい(注:1番目のシミュ レーションの実行には、数分かかるかもしれません)(注:あまり大きい図(画面全面に広がる図とか)にはしないでく ださい)