![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
【ここをクリック】←左のリンクのページに入り、画面の説明に従って、データを入力してください。今回の復習課題に使います(間違った形式で入力すると、処理が複雑になりますよ)。入力が同じ時間に集中すると「更新の衝突」がおきます。「コメントの挿入」ボタンをクリックする直前に、一度、ページをリロード(再読込)しておいてください。
これまでは主にExcel, Word, Power Pointなど、お金を出して買わなければならないソフトウェアの使い方を勉強してきました。でも、これらを個人で購入しようとすると、アカデミックパッケージを買っても数万円します。自分でパソコンを買った人にとって、こういうソフトを揃えるだけでもけっこう大変なことでしょう。
一方、講義で使ったK2EditorやWinShotはフリーソフトです。こういうソフトウェアは、作者が趣味で作ったり、自分のために作ったものを、無料で公開してくれている場合が多いです。作者の努力と親切さに感謝の心を持って、有りがたく使わせていただきましょう。
そして、近年のインターネットが発達に伴って爆発的に広まってきた物が、オープンソースというものです。ここでいう「ソース」というのは、もともとはプログラムの核となる「ソースコード」(文字で書かれた大元のプログラムリストと考えていい)のことを言っています。「オープンソース」では、大元の「ソース」が無料で公開されているので、それを見て、改良点を思いついた人が、自由に改良することができます。あるいは、そういうプロジェクトを立ち上げれば、不特定多数の人が意見を交換し、協同作業で改良を加えることで、どんどん素晴らしいものができあがります。
「無料だったら、大したものは無いんじゃない?」などという声が聞こえてきそうですが、そんなことは無いです。コンピュータを動かす核であるOSの一つ、Linux (この教育用計算機システムでも利用可能だし、授業のウェブサーバーでもOSとして使っている)は、オープンソースで大成功を収めた例です。
今後の講義では、オープンソースで配布されているいくつかのソフトウェアを用いて、統計、プログラミング、データベース等を学んでゆきます。それぞれのテーマについてはもちろん商用のソフトウェアもありますが、次のような理由でオープンソースのソフトウェアを選びました
デメリットとしては、
でも、デメリットよりもメリットの方がずーっと大きいので、皆さんもオープンソースソフトウェアに慣れ親しんでください。
日本語で描かれた情報が載っているページへのリンクのみ示した。本家はほとんど英語。
前回のアンケートの結果分かったのは、多くの人が統計解析というものが何をするのか、今ひとつイメージがつかめていない(あるいは、イメージは出来ていても、言葉にできない)ようでした。基礎からやって欲しいという意見もあったけれど、授業時間内では無理です。そこで、この授業は、Rを使ってできる実践的な統計解析をやって見ましょう。生物学を学ぶ限り、統計解析は必ず使うことになります(もう、土谷先生や仲岡先生の授業では使ったでしょ?)。理論は十分には理解できていなくても、「・・・・という解析をして得られた__という結果から、####と判断しました」と、自分の判断の客観性を、Rを使った解析で主張する方法を習得します。こうやって、まず、データとその扱いに慣れることで、統計解析に親しんでゆきましょう。そうすれば、きっと、教科書を読んで統計の勉強をするときに、イメージが湧くはずです。
この授業では統計解析を、次の2つの目的のために使います。
1. ある対象(集団)から得られた部分的な数値データから、その対象の持っている性質や特徴を知ること
2. ある対象や実験で得られた数値データを用いて、その対象についてどういう判断を下せば良いかを論じること
"ある対象(集団)から得られた部分的な数値データから、その対象の持っている性質や特徴を知ること"
生物学の大きな目的の一つに、自然界に存在する様々な生物の特徴を知ることがあります。でも、自然界の生物全部を計測して、特徴を知ることは不可能です。そこで、対象とする生物の一部だけ(標本)を取り出して特徴を計測し、対象生物全体(母集団)の特徴を推定します。こういう作業を「統計的推測」と言います。
それでは、実際に統計的推測やってみましょう。Rを使った実際の作業は皆さんが前回の予習課題でやったのと同じです。
データとしては、【ここをクリック】←ここに、産業技術総合研究所 デジタルヒューマン研究センターから提供して頂いた、1997年の男子大学生110人の身長、体重のデータがあります。このデータを使って、1997年当時の大学生の身長と体重の一般的傾向について議論してみましょう。
このとき、
母集団は1997年当時の大学生全て
標本は1997年の男子大学生110人
です。今回の統計的推測では、
110人分のデータから、1997年当時の大学生全体の身長と体重の傾向を推測する
ことを目的としています。
> h=scan() 1:画面に表示された 1: の後に、上のページから身長データをコピー・ペーストして、最後にenter キーを押します。次のように表示されるはずです。
1: 1775 1710 .. ..<省略>.. 111:同様にして、体重データも w というオブジェクトにを入れてください。次のように表示されるはずです。
1: 79.8 58.0 .. ..<省略>.. 111:確認のために
> h > wと入力してみましょう。データが一覧表示できます。
それではまず、計測したデータがどういう性質を持っているのか、目で見て分かりやすいグラフにしてみましょう。こういう場合はヒストグラム(柱状グラフ)を使って、ある範囲の身長を持つ学生が、標本全体の何割ぐらい存在するのかを示すと、データの持つ性質が直感的に理解できます。Rを使ってヒストグラムを書く場合は
> hist(h)キーボードからたった7文字打ち込むだけです。 身長の度数分布がグラフで表示されました。同じことを体重についてもやってみましょう。
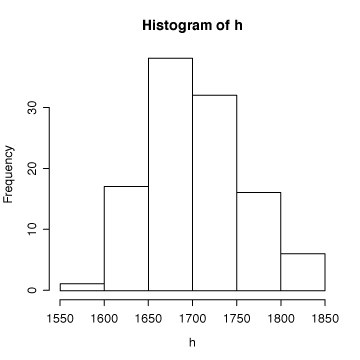
このグラフを見ただけで、標本データでは身長170cmぐらいの学生が最も多く、 データは釣り鐘型の分布をしている。ということが分かりますね。同様のことを体重についてもやってみましょう。
> hist(w)
次に、この標本データの平均とか最大値とか、最小値とか、データの集まりがもっている基本的な性質を表示させて見ましょう。次のように入力してください。
> summary(h) Min. 1st Qu. Median Mean 3rd Qu. Max. 1578 1671 1700 1706 1734 1839これで、1997年当時の調査した大学生110人の身長は、平均170.0cm(最大:183.9cm, 最小: 157.8cm)ということが分かりました。1st Qu.と3rd Qu.というのは、全体の4分の1の人数がどの高さまでの間に含まれているかということを表しています。つまり、167.1cm以下の人が25%、173.4cm以上の人が25%、その間の人が全体の50%ということです。
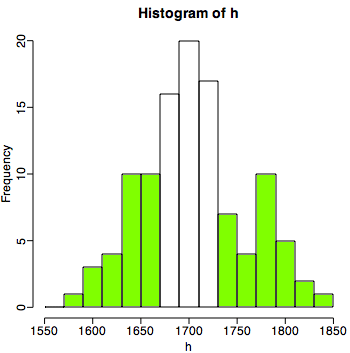
> summary(w) Min. 1st Qu. Median Mean 3rd Qu. Max. 44.20 55.10 59.40 59.53 64.40 82.20
身長も体重も釣り鐘型の分布になっていました。では、この2つの数値の間に何か、関係があるのでしょうか?これもまた、グラフで表示させてみましょう。こういう場合、縦軸に体重、横軸に身長をとって、一人一人の持つ身長と体重の散布図を作ってみます。
> plot(h,w)身長と体重の関係は右上がりの直線関係にありそうですよね。
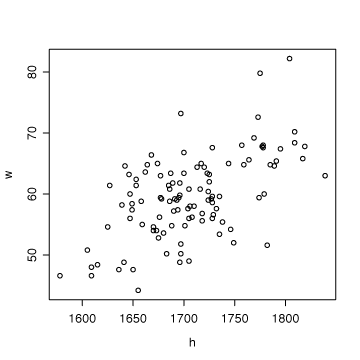
今回、110人分のデータを使って、1997年当時の大学生男子の身長と体重について、
グラフによる視覚化 要約統計量の表示 散布図の作成という3つのことを行いました。この標本が母集団の性質を表しているとするならば、1997年当時の大学生について、次のような推定ができます。
1997年当時の男子大学生は、身長の平均が170.6cmで、データは釣り鐘型に分布している 体重は平均が59.53kgで、身長と同様にデータは釣り鐘型に分布している 身長と体重の間には、正の相関がある
なお、今回は分散や標準偏差の話しは省略しました。Rを使った統計解析の基本(データの図示、代表値の計算、データ間の相関)などについてはここでは説明しきれないので、下のリンクにある中澤さんによる解説などを読んで、勉強してみて下さい。
"ある対象や実験で得られた数値データを用いて、その対象についてどういう判断を下せば良いかを論じること"
生物学科の皆さんは必ず出会うことになっています
皆さんはこれから、自然界の集団を対象にして、いろんなデータを集めるだろうと思います。例えば、千葉大キャンパス内に生息するゴキブリの体長かもしれないし、雄と雌の比率かもしれません。そういうデータに共通して言えることは、全ての個体を観察・計測することは無理だということです。そこで、私たちは千葉大の全ての対象生物からなる集団(母集団と呼びます)から、偏り無く一部を取り出して(これを任意抽出とかランダムサンプリングと呼びます)、母集団の性質を推測します。「一部を使って全体を知る」というのが統計の基本であると言って良いでしょう。

生態学などのマクロ系の生物学では、上のような方法で標本を採集し、母集団の性質の解析に統計学的手法を用いることが、非常に沢山あります。この授業では、統計学全般について語っている時間は無いので、ほんのさわりしか扱いません。下に示す参考書などを読んで、勉強しておいてください。受験で培った数学力が落ちておらず、学問に対する情熱が非常に高い、1年生の今が統計学修得のチャンスですぞ!
さて、前回の課題アンケートでは、A君とB君のジャンケンの勝ち負けの数20回分のデータから、2人のジャンケンの強さに違いがあるかどうかという質問をしました。いろんな意見が出ていましたが、(→アンケート結果)大きく分けると、4つぐらいに分かれました。
ジャンケンの勝敗は純粋に偶然で決まるので、何回もやれば必ず1:1になると判断した人たち: 10 サンプル数(試行回数)が少ないなどの理由で、結論づけられないと判断した人たち:9 データからA君の方が強い(何かの不正をしている)と判断した人たち:7 何らかの解析をもとに自分の判断を述べている人たち:5
これから話しをするのは、上の4つのうちの4番目です。つまり、たかが20回の試行であっても、5回しか勝てないというのが、偶然に起きても不思議は無いぐらいのものなのか、すごく珍しいことなのかということを判断します。
あなたは生物学科の4年生です。卒業研究テーマは「ヨコヅナサシガメの性表現について」というものです。 ヨコヅナサシガメは外来種として問題視されています。通常、集団内の雌雄の比率は1:1ですが、千葉県のある 地域の集団では、どうも、雄の方が多そうだということに気がづきました。この雌雄の差が生じた原因をつきとめ れば、ヨコヅナサシガメの防除にも使えるかもしれません。予備実験でその地域の調査に行き、あちこちで採集 したところ、20個体採集することができました。性比を調べたところ、15匹が雄、5匹が雌でした。 今後、もっと大規模な調査を計画するためにも、今回の調査結果が、単なる偶然か、それとも、その地域の集団の 性比に偏りがあるせいなのかを判断したいと思います。どうすれば良いでしょうか?
卒業がかかっているのですから、「1000個体ぐらい見ないとわからない」とか、「雄・雌は偶然に決まるに違いない」などとは言ってられなさそうです。
そこで、統計的検定の出番です。今、知りたいのは、
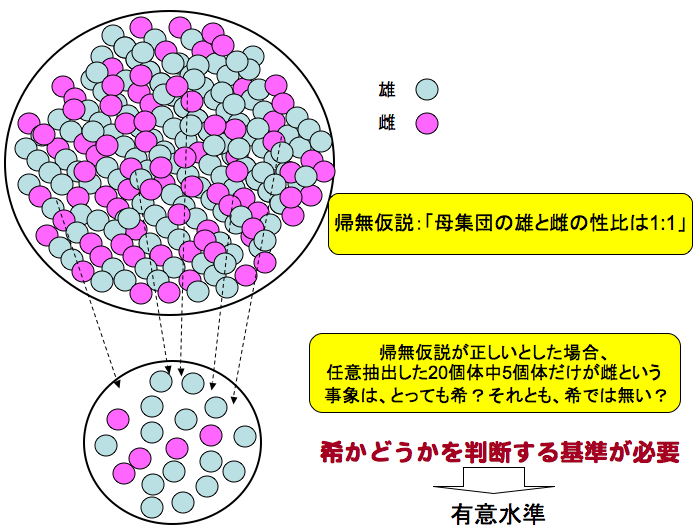
「採集したうち20匹中15匹が雄という状況は、性比が1:1の生物で、単なる偶然で起こるようなことか、 あるいは、偶然では滅多に起こらないことか」
ということです。このように、得られたデータが単なる偶然で生じることからどれだけかけ離れているかを知るには、統計的検定という作業が必要になります。
統計的検定では、次のような論証を行います。
母集団の性比は1:1であるこの仮説のことを 帰無仮説と言います。(統計の教科書を見ると、帰無仮説には「違いがない」とか「差がない」という仮説を使うと書かれています。「違いがある」とか「差がある」という仮説はつかえません。今回の場合「『母集団の性比は1:1である』というだけで「差が無い」とか「違いが無い」とかは言って無いじゃないか?」と思う人がいるかもしれません。でも、「性比が1:1である」ということは「雄と雌の出現確率には違いが無い」ということを意味しています。字面だけで判断するとこんがらがる場合があるので、注意してください。)
母集団の性比は1:1では無いということです。対立仮説は帰無仮説を否定したものになっています。
20匹中15匹が雄だったというのは、サンプリングの際の偶然のバラツキによる可能性が考えられます。つまり、「母集団の性比は1:1」であったとしても、偶然のバラツキによって、20匹中雄が15匹得られる確率を計算して、その確率をもとに、それがどれだけ起こりにくいことかを判断しようとしています。この確率の事をp値(Rではp-valueと表示される)と呼びます。
p値の計算をするときに、20匹中雄が15匹の場合だけを計算してはいけない 20匹中雄が15匹以上(15, 16, 17, 18, 19, 20)の場合の確率を計算しなくてはならないということです。この後の議論に出てくるように、起きた事象がどれだけ珍しいことかを判断して、それが滅多におこらないようなことなら、帰無仮説を棄却します。16匹以上が雄というそれぞれの事象は15匹が雄という事象よりも起こりにくいことですから、そう言う場合にも、帰無仮説は棄却されることになります。そのため、p値の計算は「15匹以上」の場合の確率が必要になるのです。この確率のことを累積確率と呼びます。
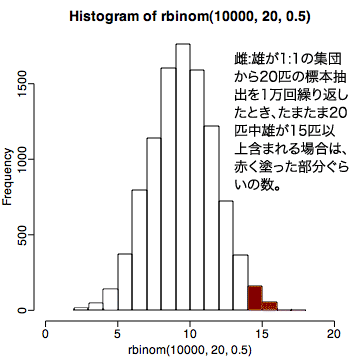
hist(xlim=c(0,20),rbinom(10000,20,0.5)) で表示させた
「母集団の性比は1:1である」(帰無仮説)(つまり、データの偏りは単なる偶然)が棄却されたのですから、
「母集団の性比は1:1では無い。」(対立仮説)(つまり、データの偏りは、単なる偶然では無い)
「母集団の性比は1:1である」(帰無仮説)が正しいという仮定の下で、「20匹中15匹が雄」という状況が生じる確率(p値)が、「希さ」の基準(有意水準)よりも大きいわけです。言い換えると、「母集団の性比が1:1であるときに、20匹中15匹が雄になるという状況は、別に不思議ではない」ということになります。つまり
「母集団の性比は1:1である」(帰無仮説)という仮説は 棄却 されないということです。得られたデータからは帰無仮説を否定できなかったので、この場合、得られたデータ(この場合、は20匹中の雄・雌の数)には、...%(...にはp値と比較した値が入る)の有意水準で、有意差が無いと言います。ここで注意しなければならないのは、「有意差が無い」からといって、「母集団の性比は1:1である」と結論づけてはいけないことです。「有意産が無い」のは、「母集団の性比は1:1であってもおかしくは無い」ということを意味しているだけで、単なる偶然の結果かもしれないし、データ数が少ないせいかもしれないし、いろんな場合があり得ます。
では、実際に先ほどの例を解析してみましょう。この検定は二項検定と呼ばれています。まず、帰無仮説は
母集団の性比は1:1である
ということです。この帰無仮説が正しいと仮定すると、 得られたデータの偏りは、サンプリングの際の偶然の偏りであると考えられます。確率50%で生じる事象が、20回中15回得られたわけですよね。検定の際には、これより希な条件も全て含めて確率を計算します。つまり、20回虫、15回以上その事象が生じる確率を計算します。 手で計算してもいいのですが、今回はすぐにRを使ってみましょう。上の検定を行うにはbinom.test()関数を使います。
> binom.test(x,n)
と入力するだけで、実際のx個のサンプルの中で、データ値がn回実現したという状況で、そのデータ値は(もう一つの対になるデータ値に対して)母集団中で1:1で出現するという帰無仮説をテストできます。
このテストの説明はそんなに難しくないです。20回中、雄が15回以上生じる確率を計算してみてください。詳しい解説は、上記、粕谷さんのピンク本に載っています。
上の例だと、20サンプル中15サンプルが雄で、帰無仮説は「母集団の性比は1:1」だということでしたから、
> binom.test(15,20)
Exact binomial test
data: 15 and 20
number of successes = 15, number of trials = 20, p-value = 0.04139
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.5089541 0.9134285
sample estimates:
probability of success
0.75
p値の値は0.04139なので、有意水準が5%の場合は、有意水準よりも小さい値だということです。なので、帰無仮説「母集団の性比は1:1である」は棄却されます。(もちろん、有意水準を0.001にすると棄却されません)
つまり、調査した地域のヨコヅナサシガメの母集団には、有意水準5%では、雄と雌の性比に偏りがあったということができます(有意水準0.1%の場合は、「性比に偏りがあるかどうか分からなかった」)。有意水準5%では、性比が1:1という帰無仮説は棄却されたという言い方もあります。
どうやらその地域のヨコヅナサシガメの母集団には性比に偏りがありそうなので、卒業研究の調査をすすめても良さそうですね。
今回の解説では、片側検定、両側検定の話しは意図的に省略してあります
先ほど1997年の男子大学生110の身長データをhというオブジェクトに入れました。【ここをクリック】のもう少し下の方には、1998年当時60歳以上の男性51人の身長のデータものっています。大学生(平均20.52歳)と60以上(平均68.61歳)では、48歳ほどの差があります。同じ成人男性といったって、40年も違う時代に成長期を迎えたわけですから、身長には違いがあってもおかしく無いような気がします。この2つのデータをみて、2つのサンプルの母集団(ランダムサンプリングが行われたとして、1997年当時の男子大学生全てと1998年当時の60歳以上の男性全て)の間で身長には差があると言っても良いでしょうか?
60歳以上の男性の身長データをオブジェクトに格納します。scan()関数を使って
> h2=scan() 1: 1547 1689 .. ..<省略>.. 52:
hとh2のそれぞれの平均値やヒストグラムを比べてみてください。
> summary(h) > summary(h2) > hist(h) > hist(h2)
平均値やヒストグラムを見た限りでは、けっこう違いがありそうです。
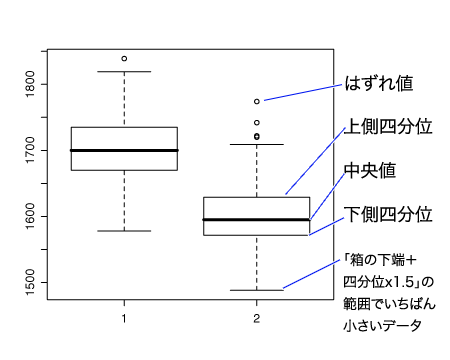
もう一つグラフを作ってみましょう。2集団のデータを簡単に比較するときに便利な関数が、boxplot()です。
> boxplot(h,h2)
さて、いよいいよ検定です。検定の考え方は上で示したのと全く同じです。ただし、データの持っている性質が違うので、p値の計算方法は異なってきます。このような2集団の違いの検定には、Wilcoxonの順位和検定という方法を使います。検定の説明はブラックボックスになりがちですが、上で紹介した粕谷さんのピンク本や、中澤さんのRの使い方pdfには、詳しい考え方の説明がかかれていますから、読んでおいて下さい。今回はRを使った統計的検定がいかに楽かということを示すのが目的なので、詳しくは触れません。
まず、ヨコヅナサシガメの例で見たように、帰無仮説と対立仮説を決めます。
帰無仮説: 2つのサンプルの母集団の身長に差は無い 対立仮説: 2つのサンプルの母集団の身長に差はある
2つの母集団に違いがなければ、hとh2という集団のデータは、母集団から抽出したときに、たまたま偶然で偏ってしまったものでしょう。そういう偶然の偏りでこれだけの違いが生じるのは、どのくらいの確率(p値)で生じるのかを計算します。Rではwilcox.test()という関数を使います。
> wilcox.test(h,h2) Wilcoxon rank sum test with continuity correction data: h and h2 W = 4957, p-value = 5.329e-15 alternative hypothesis: true mu is not equal to 0
p値の値は 5.329e-15 で、これは 5.329x10^(-15) を示しています。つまり、0.0000000000000005329です。これは有意水準の0.01%よりもずーっと小さい値なので、2つの身長データの違いが同一母集団から偶然のサンプリングのバラツキでで生まれたということはほとんど無い、ということを示しています。統計学っぽく表現すると、「2集団の差をWilcoxonテストで検定した結果、0.01%の有意水準で有意な差があった」と書きます。
どうやら、40年も年齢の異なる2つの母集団の身長には差があると言って良さそうです。やっぱり、成長期に摂取できた栄養の影響などが、きっと大きいのでしょう。
さて、いつもじゃんけんに負けてしまうB君。お父さんや母さんに聞いても、「そのうちきっと続けて勝つよ」と、取り合ってくれません。どーしても、納得行かないので、隣町に住む、いとこのあなた(理学部生物学科の学生)に相談に来ました。「僕にとってはしかつ問題なんだかね」と言うB君。"むつかしい"言葉を使うのが好きなおませさんです。
そこで、あなたは、なんとかB君にも分かるように説明してみました。
「B君は、A君がなにかずるをしていると思ってるんだよね?だって20回じゃんけんをして、15回もA君が勝っちゃうんだからおかしいよね。でもA君は、じゃんけんは偶然で決まるんだから、1000回もやればそのうち勝率は半々になるって言うんでしょ?じゃんけん1000回かー。そのくらいやれば、2人とも大人になっちゃうね。
まあ、ともかく、仮にA君が言うように、じゃんけんはでどちらが勝つかはホントに半々で決まるとしてみようよ。
20回のうち10回勝つことは、ありそうだよね。
20回のうち11回勝つことも、ありそうだよね。
12回勝つことは、まあ、ありそうかな。
13回や14回だと、ちょっと微妙?
それで15回だと、。。。ありそうにないって感じるわけでしょ?
いいかい?今、「じゃんけんでどちらが勝つかはホントに半々で決まる」と仮に考えているよね?そのとき、
A君は、「半々で決まるのだから、20回中15回勝つことはそんなに珍しいことじゃない」
B君は、「半々で決まるんだったら、20回中15回勝つなんて珍しいことが起こるのはおかしい」
2人の主張が食い違ってるわけだ。だったらさ、「勝敗が50%の確率で決まるとき、20回中15回勝つこと」が、どれだけ珍しいことか、測ってみればいいんじゃない?こういうのって、確率で測れそうだよね。
じゃあ、「勝敗が50%の確率で決まるときに、20回中15回勝つ」確率を計算してみよう。
その確率がそんなに小さく無いのなら、「勝敗が50%の確率で決まるときに、20回中15回勝つ」ことは、別にあっても不思議じゃ無いっていうことでしょ?
逆に、その確率がとーっても小さいなら、「勝敗が50%の確率で決まるときに、20回中15回勝つ」ことは滅多に起きないということなので、きっと「勝敗が50%の確率で決まる」っていう前提が間違ってるよね?
(なんと、B君は、この難しい説明を理解したようです。)
どうやってその確率を計算するかって言うと....うーん、一つ一つ説明するのは大変だから、ここはパソコンにやらせよう。ほら、このRというソフトを使うと、
binom.test(15,20) Exact binomial test data: 15 and 20 number of successes = 15, number of trials = 20, p-value = 0.04139 alternative hypothesis: true probability of success is not equal to 0.5
こうなって、p-valueっていうのが、「勝敗が50%の確率で決まるときに、20回中15回(以上)勝つ」確率なんだよ(注:話しが難しくなりそうなので、累積確率の説明は端折ったようです)。そうすると、0.041っていうことは、4%ぐらいの確率だよね。どう?「勝敗が50%の確率で決まるときに、20回中15回(以上)勝つ」のは、100回中4回しか起きないっていうことなんだよ。やっぱり低いって思う?
今やったような計算を統計的検定って言うんだけど、問題にしていることがどれだけ起こりにくいかを議論するときには、5%とか、0.1%とか、0.01%っていう基準を使うんだ。まあ、よく使われる、「珍しさ・起こらなさ」を示す基準のうち一番大きいのが5%だね。B君のジャンケンの例だと、「勝敗が50%の確率で決まるときに、20回中15回(以上)勝つ」確率が4.1%だったでしょ?5%っていう基準よりも小さいので、「滅多に起きない」って言っていいわけ。つまり、「勝敗が50%の確率で決まる」っていう前提が間違いだと考えられるので、きっとA君が、何かずるをしている可能性が高いだろうと考えられるんだよ。でも、珍しさの程度はあくまでも、4%、つまり、100回中4回ぐらいは起きても構わないってことだからね。A君が言うように「勝敗が50%の確率で決まる」ってことは絶対無いなんて言える訳じゃないからね。
さすがのB君も、確率とか統計とかが出てくるとこんがらがってきたようです。
ともかく、A君がずるをしているのかも知れないという可能性を、何だか難しい話しで説明してもらったB君、少しは納得できたようです。ついでに、どうすればずるをされなくなるか、聞いてみました。何回か一緒にジャンケンをしてみたところ、手や体の動きに癖は無さそうです。そうすると、きっと、出し方のパターンを覚えられてるのだろうという事になり、乱数表をおみやげに貰いました。ジャンケンをする前に、この表をこっそり見て、何を出すかを決めるそうです。。。。
php-4.4.2-Win32 xitami-25
php xitami
./09
良くある間違い: joho19/07s9999/06 というページを作るべきなのに joho19/07s9999/05/06 としてしまったとか
*第9回授業アンケート **氏名: -今日(6月15日)の授業の進み方は?(はやい、丁度いい、おそい) --回答: -今日の授業の難しさはどう感じましたか(簡単すぎ 簡単 丁度いい 難しい 難しすぎ): --回答: -難しいと答えた人は、特にどの点が難しかったですか?: --回答: -今日の授業は(よく分かった 分かった 分からなかった): --回答: -分からないと答えた人は、特にどの点が分からなかったですか?: --回答: -今日の講義で理解できなかった用語があったら挙げてください: --回答: -この授業では大量のデータをいかに効率良く処理するかということに注目しています。 そこで、次の質問に答えてください。 -これまでの人生で、自分が扱った最も大きなデータの規模を答えてください。例えば、 名簿の場合人数と項目、実験データの場合、何件のデータとか。 --回答: -今後の大学生活で、自分がどのくらいの大きなデータを扱うことになるか、データの種類と規模を 想像で答えてください。 --回答:
問1:生物学科1年男子学生の身長のsummary()の結果をペーストしなさい: 問2:生物学科1年男子学生の体重のsummary()の結果をペーストしなさい: 1997年男子大学生110人と、生物学科1年男子学生の身長のデータは、それぞれが、当時の大学生の集団から、 任意にサンプリングされたものだと仮定します。このとき、両者の母集団の身長に差があるかどうかを 検定します。 問3:帰無仮説は何ですか?: 問4:対立仮説は何ですか?: 問5:検定に用いたRの計算式と結果をコピー・ペーストしてください (以上、全て、回答を書くときは、1行ずつ、行頭に半角スペースを入れること) 問6:検定の結果からどのようなことが議論できますか?: