授業/H26/情報処理/11

Rを使ったプログラミング演習2：　シミュレーション †

はじめに †

Rでシミュレーションの授業を始めたころ、受講生から次のような質問があった。

「シミュレーションのプログラミングって、これから生物学を学ぶのに、どのくらい必要なんですか？」

これまでプログラミングなどしたことの無い人にとって、とても素直な疑問だろう。私からの答えとしては、

シミュレーションそのものが直接必要になるような分野もあれば、そうでない分野もあります。
プログラミングは、生物学における発展的な情報処理として、とても重要なものだと思います。
将来、数理生物学、理論集団遺伝学、進化生態学、バイオインフォマティクスを志す人には、
必須技術といっても良いでしょう。

ということで、今回は、Rを使ったシミュレーションに挑戦してみよう。

第11回授業の獲得目標： †

• 1. プログラミングの基本：繰り返し・代入・条件分岐に習熟する
• 2. ユーザー定義関数を理解する
• 3. シミュレーションの考え方を習得する
• 4. シミュレーションのプログラミングを体験する
• 5. 遺伝的浮動のシミュレーションに挑戦する！

おさらい0：演習・グループワーク　プログラミングは手順書き！　 †

前の授業で、「プログラミングは数学というよりも、コンピュータにことばで手順を伝えることだ」という説明をした。
例えば、おつかいに行く子供に、次のような買い物の手順を説明して、お使いの後、財布の中に残っている金額を表示させるプログラムを考えてみよう。

お財布の中に500円入っているから、これを持って買い物に行ってね。
この通りをまっすぐに進むとお店が３軒あるから、
最初のお店で、100円のゴーヤを１本もらって、100円を渡すんだよ。
次のお店で100円のお豆腐を一丁もらって、100円を渡すんだよ。
次のお店で100g 100円の豚肉を、200gもらって、200円を渡すんだよ。
残ったお金はいくらだった？（あとでお菓子をかってもいいよ。）

このお買い物の手順を、先週学んだ「繰り返し・代入・条件分岐」 を使っておおざっぱに表現してみると、どうなるだろうか？
グループで相談しながら、考えてみよう。
相談しおわったら、授業moodleサイトにアクセスしよう。一例をしめしておいた。

• ヒント：以下のような命令を組み合わせれば良い（変数名に日本語を使うこともできる）
  • お財布の中のお金:

    お財布の中 = 500

  • お買い物を3回行う

    for (i in 1:3) {  #３回買い物を繰り返す
     ＜お買い物を表すプログラム＞
    }

  • お買いものでお金を使う部分

        if (i == 1) {    #iの値で何件目かを表す。3件目以外は100円ずつ使う
          　　＜「お財布の中」がどう変化するかを表現＞
        }

  • 「お財布の中」を表示

    print(お財布の中)

このプログラムの中に含まれている「繰り返し・代入・条件分岐」 の働きを、十分に理解しておこう。

おさらい1：　プログラミングの基本：　繰り返し・代入・条件分岐 †

次のそれぞれのプログラムの＿部分に何を入れるべきかを選択肢から選びなさい。また、Rを使って実行してみよう。

繰り返し †

• 演習： 1から10までの数字を表示させるプログラムを作りなさい

  for(i in 1:__){    #{と}の間を10回繰り返す。i の値は毎回1ずつ増える
    print(i)
  }
  
  選択肢： a) 1    b)  5     c)  10
  簡単にできた人は、結果を横一列に表示させてみよう。

代入 †

• 演習： 1から10までの数字の合計を計算するプログラムを、for文を使って作りなさい

  goukei=0           #goukeiという変数に初期値0を代入
  for(i in 1:10) {   
    goukei=_____+i  #goukeiに前回までのgoukeiの値にiの値を足したもの代入
  } 
  print(goukei)
  
  選択肢： a) i    b)  goukei   c)  print

条件分岐 †

• 演習： 1から10までの数字のうち、2の倍数だけを合計するプログラムを、for文とif文を使って作りなさい

  goukei=0           #goukeiという変数に初期値0を代入
   for(i in 1:10) {
     if(i %% 2 __ 0) { # %% は割り算をした余りを返す演算子。3 %% 2 の計算結果は 1 になる
       goukei=goukei+i # if文の内容は：　「もし i を 2 で割った余りが 0 ならば、{}内を実行
     }               #それ以外は何もしない
   }              #for 文のカッコ閉じるに注意
   print(goukei)
  
  選択肢： a) =    b)  ==     c) <=

プログラミングTips †

・１行に１つの命令を書いたら、必ず改行
・{  }  のそれぞれの後で改行すると見やすい（このページの例を参照）

おさらい3：ユーザー定義関数 †

「ユーザー定義関数」というのは、関数を定義する関数function()を使って、自分で作成したプログラムに名前を付けるようなものだった。オサライのため、１つ演習をしておこう。

• 演習：　#穴埋め式練習問題: _の部分に適当な文字を入力して実行しよう

  #入力した回数だけ乱数を1つ発生させて、それが0.5より小さいものだけを抜き出して表示させる
  ransu=___(a){   #ユーザー定義関数を定義
   kekka=c()     #結果をいれておく空ベクトルを作る
   for (i in 1:_) {  # a 回繰り返す
    x = __(1)           #乱数を1つ発生させる
    if (x  < 0.5 ) {   #発生させた乱数が0.5より小さいならば
       kekka=c(kekka, x)
    }
   }
   print(kekka)
  }

ransu(50)
などと入力すれば、0.5より小さい乱数がいくつか表示される

おさらい4. 授業で使ったRの基本関数 †

→授業/H20/情報処理/R関数一覧　　これまでに学んだRのいろんな関数を一覧できる。

Rを用いたシミュレーション †

これまでに学んだ繰り返し・代入・条件分岐の３つの命令それぞれは単純だが、組み合わせれば、かなり複雑で、研究に役立ちそうなことでも表現できる。そこで、今回は、これらの命令を組み合わせて、Rを用いたシミュレーションに挑戦してみよう。
シミュレーションという言葉は「株式シミュレーション」とか「シミュレーションゲーム」とかで聞いたことがあるだろう。日本語にすると、「模擬実験」で、自分では実行が難しい繰り返し実験を、コンピュータに計算させることで行うものだ。コンピュータは単純な繰り返し計算は得意なので、砂粒をばらまいて、ある図形の中に入った数を数えるなんていう作業を、10万回でも、100万回でも繰り返すことができる。下の例では、実際に、ある図形の上に砂粒をまく実験をコンピュータに繰り返し行わせるシミュレーションを行って、円周率（π）の値を求める。
この例ように、シミュレーションをうまく使えば、たとえ数学的に解くのが難しい問題についても、近似解を求めることができる。また、ある生命現象について、自分で作成したモデルを用い、パラメーターの変化がどのような状態の変化をもたらすかを予測することができるため、進化生物学や生態学でもよく使われる。２つめのシミュレーションでは、遺伝的浮動のシミュレーションをやってみよう

円周率(π）を「繰り返し」・「乱数」・「条件分岐」で求める †

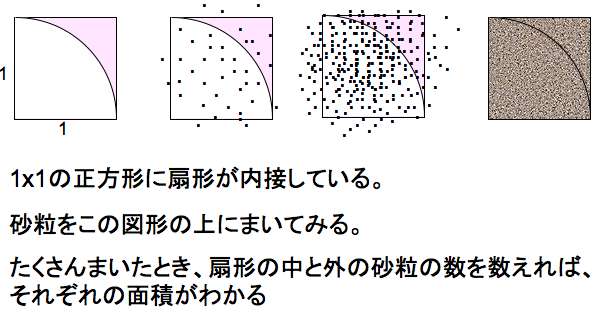
左に１辺の長さが1の正方形と、それに内接する扇形がある。このとき、

正方形の面積は　 1　　扇形の面積は       π/4

この図形の上に、砂粒をばらまいてみる。 砂粒が図形の上にランダムに散らばるとすると、砂粒をすごく沢山まいて数を数えれば、

正方形の中の砂粒の数(n) ： 扇形の中砂粒の数(m)  ＝　
正方形の面積 ：扇形の面積 ＝
１　：　π/4

になると考えられる。つまり

   n : m = 1 : π/4　　　だから、   π = 4m/n

もしあなたが、砂粒をたくさんランダムにまいて、正方形の中の砂粒と扇形の中の砂粒の数を数えることができれば、πの値がわかるということになる。自分で実際に実験することを想像すると、恐ろしく大変だが、そういう面倒な実験はコンピュータにやらせてしまえばいい！

シミュレーションの考え方 †

• 砂粒をたくさんまく部分
  さて、砂粒を沢山まいて、それが円の中か外かを判定する実験を、コンピュータにやらせるにはどうすればよいだろうか。 まず、点（砂粒）を大量に発生させる必要がある。さて、どうすればいいだろうか？
  もうお分かりのように、「繰り返し」命令（for文）を使う。

  #とりあえず、1,000つぶの砂をまくことをfor文で表現する
  for (i in 1:____){
   print(i)  #＜砂を１粒図形の上にまく＞
  }

• 砂粒をランダムにまく部分
  次に、砂を１粒図形の上にまいて、それが扇形の中か外かを判定することを考える。
  

砂を１粒まくことは、無作為に（ランダムに）図形の上に点を打つことと同じことだ。先週学んだ、runif() という乱数を発生させる関数を使えば、図形の上に１つの点を打つことは、２つの乱数を発生させることで表現できるだろう。

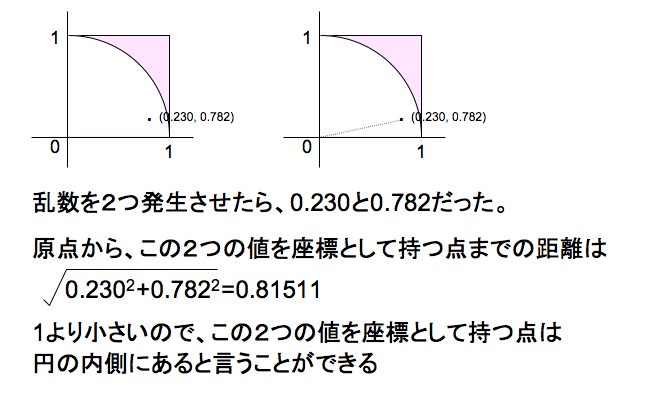
例えば、0-1の範囲の乱数を２つ発生させたら、　(0.230 , 0.782) という２つの数字が得られたとする。この２つの数字が座標上の点を表していると考えると、上の図のようになる。
原点からこの点までの距離が1より小さいとき、この点は扇形の中に入っているということができる。
Rでは平方根を表すとき、　sqrt()という関数を使うので、この例では、

sqrt(0.230^2+0.782^2) < 1

となり、ランダムに発生させた（図形の上に偶然落ちた）1つの点は、扇形の中だったということになる。
実際に２つの乱数を発生させて、それを、pointというオブジェクトに代入するには、次のようにする。

point=runif(2)  #この命令で、0-1の範囲の乱数を２つ発生させ、pointというベクトルに入れる

このとき、pointに入ったそれぞれの値を指定するには、

point[1]
point[2]

のようにカギ括弧［］を使う。

例：　[]の使い方を、試してみよう
        > x=runif(2)
        > x
        > x[1]
        > x[2]

• 砂粒が扇形の中か外かを判定する部分
  砂粒（点）が扇形の中かどうかを判断するにはどうすれば良いか？これは条件分岐で表現できる。つまり、runif(2)で発生させた２つの数値のそれぞれを2乗して足しあわせたものの平方根が1より小さいか否かを判断する。

  #扇形の中かどうかを判断する条件文
   distance=sqrt(point[1]^2+point[2]^2)   #発生させた２つの乱数の２乗の和の平方根
     if(distance<1){　　　　　　#原点からの距離が1より小さければ扇形の中
         ＜個数を数える＞
    }

• 砂粒の数を数える部分
  では、個数を数えるにはどうすればよいか？ここでは代入文を使う

   #個数を数える部分
   kaisu=0   #回数を数えた結果を入れる場所なので、最初の値（初期値）は0にしておく
     if(distance<1){　　　　　　#原点からの距離が1より小さければ扇形の中
         kaisu = kaisu + 1   #条件にあったとき、kaisuの値を1増やす
    }

以上のように、これまでに学習した、繰り返し、条件分岐、代入で、図形の上に砂粒を1000個まく実験が表現できた。πの値は砂粒の個数を4倍して、全体の個数で割ったものだから、以上をまとめると次のようになる。

	kaisu=0;  #個数の初期値を0にする
	for (i in 1:1000) {
		point=____(2)
		____=sqrt(point[1]^2+point[2]^2)
		if(distance<1){
			kaisu=kaisu+1
		}
	}
	answer=4*____/1000
	print(answer)

さらにユーザー定義関数：function()を使って、好きな回数繰り返せる関数を定義してみよう

simpai=function(x){
	kaisu=0;  #個数の初期値を0にする
	for (i in 1:x) {
		point=runif(2)
		distance=sqrt(point[1]^2+point[2]^2)
		if(distance<1){
			kaisu=kaisu+1
		}
	}
	answer=4*kaisu/x
	print(answer)
}
> simpai(10)
[1] 2.8
> simpai(100)
[1] 3.16
> simpai(1000)
[1] 3.156
> simpai(10000)
[1] 3.1624
> simpai(100000)
[1] 3.15652
> simpai(1000000)   #ここから先は時間がかかるので、授業中はやらない方がいい
[1] 3.13994
> simpai(10000000)  #ここから先は時間がかかるので、授業中はやらない方がいい
[1] 3.140556

せっかくだから、点をうつところを図で表現してみよう †

plot()関数でylimというオプションを使うと、グラフの軸の範囲を指定できる（詳しくはマニュアルを参照）

simpai=function(x){
	kaisu=0;  #回数の初期値を0にする
	for (i in 1:x) {
		point=runif(2)
               par(new=T)    #複数のグラフを重ね合わせる
               plot(point[1], point[2], ylim=c(0,1), xlim=c(0,1))  #0-1の範囲で乱数の値をプロット
		distance=sqrt(point[1]^2+point[2]^2)
		if(distance<1){
			kaisu=kaisu+1
		}
	}
	answer=4*kaisu/x
	print(answer)
}

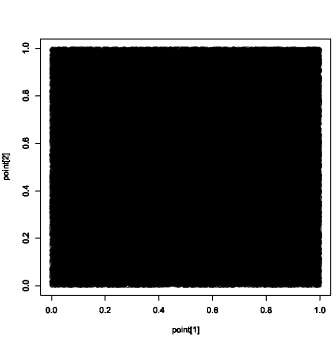
10万回の実行結果。

発展演習：　円周率の計算を乱数を使わずに行うプログラム †

• これまでの説明が分かった人は、次のような考え方でπを求めてみよう。
• 上のプログラムとよく似ているが、乱数を使わず、1x1の正方形をマス目に分割して、扇形の中に入っている交点の数を数えるもの。穴埋め問題にしておくので、プログラムを完成させてほしい。得られる値は、100のとき3.1、1000のとき3.137524、10000のとき3.14119。100000のときは計算に時間がかかりすぎて途中でストップ。

simpai=function(x){
	kaisu=0;  #個数の初期値を0にする
	for (_ in 1:_) {
		for (_ in 1:_) {
			point=c(___,___)
			distance=sqrt(point[1]^2+point[2]^2)
			if(distance<1){
			　kaisu=kaisu+1
			}
		}
	}
	answer=4*kaisu/x^2
	print(answer)
}

遺伝的浮動のシミュレーションに挑戦する！ †

次に、生物学科の学生なら、大学入試にそなえて必ず勉強した遺伝的浮動のシミュレーションをやってみよう。
遺伝的浮動とは、

大きさの決まった集団で起きる、配偶子のランダムサンプリングによる遺伝子頻度の変動

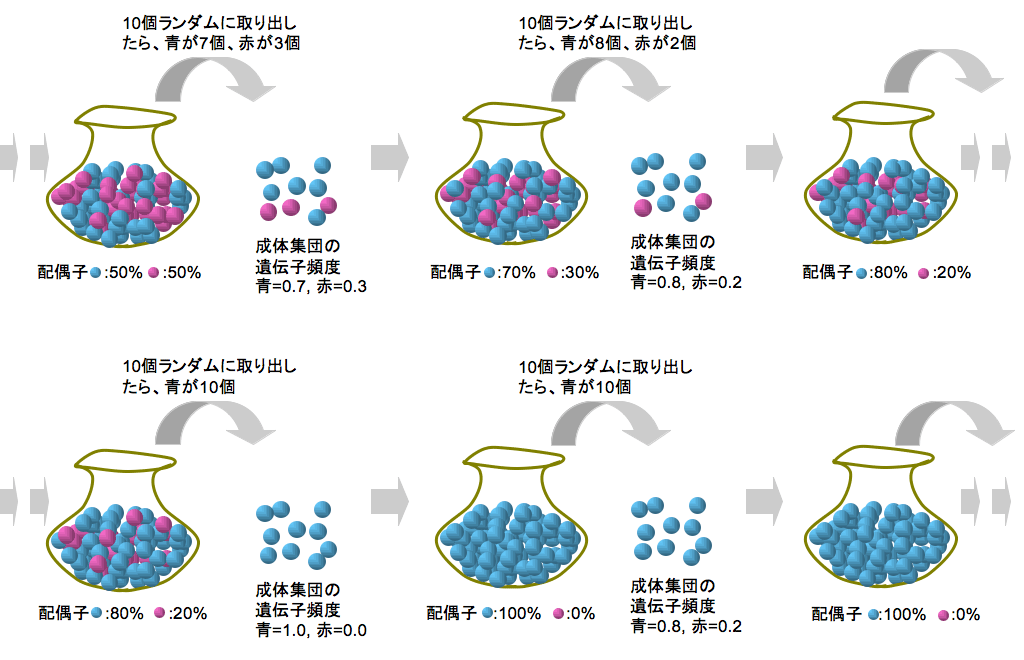
のことだ。例えば、集団中の２つの対立遺伝子を、青玉と赤玉で表すと、袋（配偶子の集団：　配偶子の数はものすごく多く、青と赤の比率はそれぞれ50%）から取り出される青玉・赤玉の割合（集団中の遺伝子頻度）には、下の図に示したような変動が生じる（下の例で、青玉の遺伝子頻度は、0.8, 0.7, 1.0, と変動している）。もし、袋から取り出されたのが青玉ばっかり（あるいは、赤玉ばっかり）だと、それ以降、何度繰り返しても変化は生じない（下の例だと、「集団は青玉に固定した」などという）。

出席確認演習＋グループワーク：　0か1に固定するまでの世代数 †

まず、上のような袋と玉をつかった実験を手作業でやった場合、取り出した玉が赤か青かどちらか１色になってしまうのは、何回目だろうか？下の条件それぞれで、グループで相談してみよう。また、相談後に自分が考えてた固定までの回数を、授業Moodleページの出席確認演習に記入しよう。

• 最初、袋の中の青玉と赤玉の数は同数で、袋から取り出すのは10個
• 最初、袋の中の青玉と赤玉の数は同数で、袋から取り出すのは100個
• 最初、袋の中の青玉と赤玉の数は同数で、袋から取り出すのは1000個

遺伝的浮動のシミュレーションの学び方 †

では、上で説明した実験を、これまでに習った繰り返し、代入、条件分岐というプログラミングの基本技を使って表現してみよう。
ここで、実験をどうやって表現するするかが、プログラミングの重要なポイントだ。この解説では、まず最初に完成版ではあるが、部分的に抜け落ちのあるプログラムをお見せする。このプログラムを見て、シミュレーションの働きを考え、完成させて、実際にシミュレーションを行ってみよう。

演習・グループワーク：　遺伝的浮動のシミュレーション：　完成版（ただし、一部、抜け落ち） †

下のプログラムは遺伝的浮動をシミュレートするRのプログラムだが、一部、抜け落ちている。また、このプログラムでは、頭の中での置き換えを簡単にするために、オブジェクト（変数）名が、日本語で表示されている。

• 観察集団数: このシミュレーションで観察する独立した集団の数
• 観察世代数: １集団について観察する世代数
• 玉の総数: 取り出した玉の数。集団内の遺伝子数に相当）
• 青玉の初期数: 0世代目の玉の総数中の青玉の数. 集団内の対立遺伝子aの数に相当）

これらの値を与えて実行すれば、ランダムに選ばれた遺伝子が、次世代の集団の遺伝子頻度にどのように影響するかを、シミュレートする観察集団数の数だけ、色つきの折れ線グラフで表示することができる。

• 問1. 下のプログラムの下線部には、観察集団数、観察世代数,　玉の総数,　青玉初期数　のどれかが入る。どれが、どこに入るかを、グループで相談してみよう。
• 問2. 上の出席確認演習でやった、３つの条件のシミュレーションを、10集団について、100世代、観察してみよう。
  • 玉の数10個の場合：　 drift(10,100,10,5)
  • 玉の数100個の場合： drift(10,100,100,50)
  • 玉の数1000個の場合： ＜自分で考えること＞
• 問3. 2008年度前期試験に出た問題のシミュレーションをやってみよう。地球上からマラリアが撲滅され、鎌状赤血球貧血症で死ぬことも無くなった場合のHbs遺伝子の頻度の変化を考える問題。集団サイズ:1万人（遺伝子の集団サイズ20000）、Hbsの遺伝子頻度:約0.1、 世代数: 100。

drift = function(観察集団数,観察世代数,玉の総数,青玉初期数){
	 結果 = c()     #結果を入れる空ベクトルを準備
	 for( i in 1 : ________ ){
		  青玉の数 = ________     #青玉の数は観察集団が代わる度に初期値に戻す
		  for( j in 1 : ________ ){
		      結果　=　append(結果, 青玉の数 / 玉の総数)   #青玉の頻度を「結果」ベクトルに入れる
                            　#最初の繰り返しでは青玉の初期頻度が入る
		      青玉計数 = 0     #袋の中の青玉の数を青玉計数に入れる。初期値は0
		      for( k in 1 : ________ ){
                   　　　　　   if (runif(1) < 青玉の数 / 玉の総数 ){  #「青玉の数/玉の総数」は青玉の頻度
			           青玉計数 = 青玉計数 + 1  #青玉計数の値を1つ増やす（青玉を数えるということ）
                    　　　　　  }
		       }
		       青玉の数 = 青玉計数   #次の世代の袋の中の「青玉の数」に、今数えた「青玉計数」を入れる
		  }
	 }
	 結果の表 = matrix(結果, nrow = 観察世代数, ncol = 観察集団数)
	 print(結果の表)
	 matplot(結果の表, type="l", ylim=c(0,1))
}

遺伝的浮動のシミュレーションの解説 †

上の演習問題の答えは、以下の囲みのようになる。以下、画像を使って、このシミュレーションプログラムを、「繰り返し」、「条件分岐」、「代入」のそれぞれについて見て行こう。

drift = function(観察集団数,観察世代数,玉の総数,青玉初期数){
	 結果 = c()     #結果を入れる空ベクトルを準備
	 for( i in 1 : 観察集団数 ){
      　　　　　　　　　青玉の数 = 青玉初期数     #青玉の数は観察集団が代わる度に元に戻す
		  for( j in 1 : 観察世代数 ){
		      結果　=　append(結果, 青玉の数 / 玉の総数)   #青玉の頻度を「結果」ベクトルに入れる
                            　#最初の繰り返しでは青玉の初期頻度が入る
		      青玉計数 = 0     #袋の中の青玉の数を青玉計数に入れる。初期値は0
		      for( k in 1 : 玉の総数 ){
                   　　　　　   if (runif(1) < 青玉の数 / 玉の総数 ){  #「青玉の数/玉の総数」は青玉の頻度
			           青玉計数 = 青玉計数 + 1  #青玉計数の値を1つ増やす（青玉を数えるということ）
                    　　　　　  }
		       }
		       青玉の数 = 青玉計数   #次の世代の袋の中の「青玉の数」に、今数えた「青玉計数」を入れる
		  }
	 }
	 結果の表 = matrix(結果, nrow = 観察世代数, ncol = 観察集団数)
	 print(結果の表)
	 matplot(結果の表, type="l", ylim=c(0,1))
}

• 繰り返し
  
  このプログラムで、は繰り返しが3重になって使われている。
  • 一番外側の繰り返し：　観察集団の数だけ繰り返す。　例えば、一連の観察を3つの集団について行いたければ、観察集団数は3になる。そのとき、結果として得られるグラフの数は3になる。1つの集団だけについて実験したいのなら、この繰り返しは必要無い。
  • 2番目の繰り返し: 観察世代数だけ、その内側（3番目の繰り返し部分）の実験を繰り返す。2番目・3番目の繰り返しは、遺伝的浮動のシミュレーションの根幹なので、省略できない。
    もし、観察世代数が100の場合、次の図の薄緑色の囲みで説明されている部分に相当する。
    

    
    

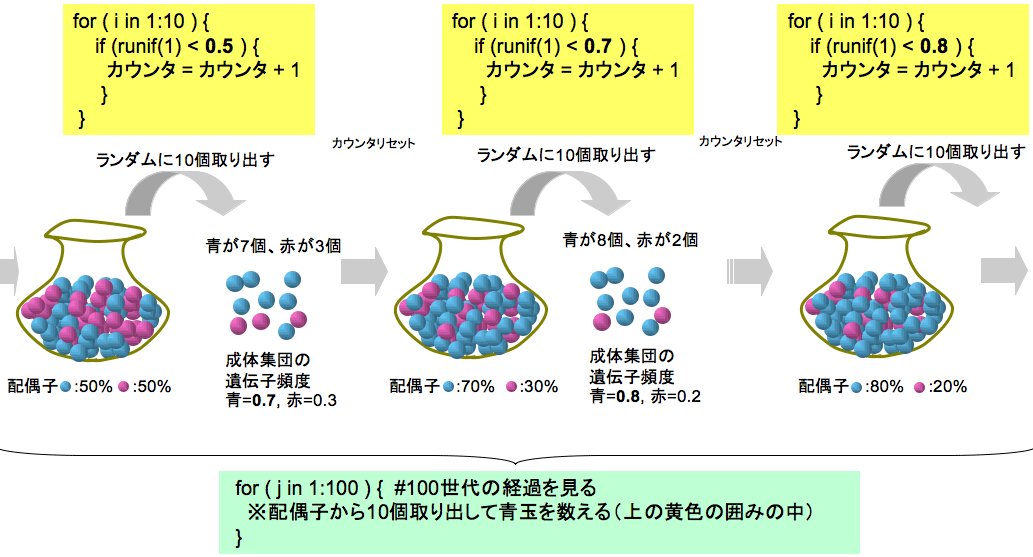
  • 3番目の繰り返し： 玉の総数だけ、実験を繰り返す。袋から、「玉の総数」で示された回数だけ玉を取り出し、青色の玉の数を数えるという実験。
    3番目の繰り返しでは、条件分岐を使って、青玉の数を数えるという操作を行っている。

• 条件分岐
  
  
  • この条件分岐で行っているif文が表すのは、「もし、取り出したのが青玉だったら、数をかぞえる」という操作だ。この部分は、遺伝的浮動のシミュレーションの最重要ポイントの１つだ。
    ここでは、これまでに学んだrunif()という関数を使って乱数を発生させて、袋から取り出した玉が青かどうかをシミュレートしている。

    
    つまり、

    0-1の範囲の乱数を１つ発生させる。
    それが袋の中の青玉の頻度（「青玉の数」÷「玉の総数」で表される）よりも小さい値だったら、
    青玉が取り出されたとみなす。上の図では、青玉の頻度が50%の場合が説明されている。~

    あるいは、こんな説明でも良いかもしれない

    例えば、袋の中に100個の玉が入っているとき、
    青には0-49の、赤には50-99の数字を書いておく
    袋から玉を一個とりだして、書いてある数字が50より小さければ、青としてカウントする
     数字： 50より小さい : 青　　→　乱数： 0-0.5
     数字： 50以上    :  赤　　→　乱数： 0.5-1

    こうして、取り出した玉が青玉かどうかがわかったら、代入を使って、数を数える

• 代入
  
  このプログラムでは、上の図のように何カ所も代入が出てくるが、3番目の繰り返しの中にあるif文の中では、

  青玉計数 = 青玉計数 + 1

  という代入が行われている。こうして、上の条件分岐で、取り出した玉が青玉の場合、「青玉計数」の値を1つ増やす。これを、玉の総数だけ繰り返すことで、ランダムに取り出された青玉の数を数えることができるというわけだ。

第11回授業の課題 †

• 提出期限：7月2日水曜正午