授業/H17/系統学特論/最尤法/モデル1

課題１：最尤法とモデル：予備知識確認 †

最尤法とモデルの理解には、一定時間が経過したときに、あるサイトの塩基がどのような確率で変化するかを考える必要があります（ソフトウェアを使って系統樹を描かせるのは、マニュアルに従って操作すればできますので、こういうことを理解して無くても大丈夫です。）。これから、綿野さんのNJ法の講義ででてきたJukes Cantorのモデルで使われている確率の考え方を、順を追って説明します。文章を読んでみて、番号つきの項目ごとに理解できたか理解できなかったか、またそれについてのコメントがあれば、メールの本文に回答欄を貼り付けて提出して下さい。＜注意＞Wordの添付書類は送らないで下さい。

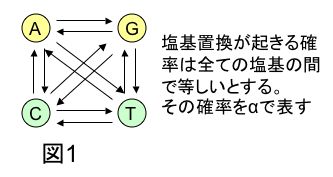
１．ある塩基配列（例えばAGGTC)のあるサイトに位置するA（アデニン）だけを例にとって考えてみましょう。今の時点を0時間目とするとき、１時間の経過後にAがT、C、Gのどれかに変化する確率は、Jukes Cantorのモデルでは全て等しいと考え、αで表します（図1）。つまり、１時間後にAがTに変化している確率はαです。また、1時間後にAがA以外の塩基（T, C, Gのどれか）に変化する確率は、T,C,Gの３つの場合に変化する確率を足し合わせたものですから、3αです。１時間の経過後に、Aが他の塩基に変化しない確率（Aのままである確率）は、1-3αです。

２．もうちょっと一般化して、t時間目の塩基の状態を考えます。t時間目にこのサイトがAである確率は、過去のサイトの状態の影響をうけて簡単には決められないので、仮にPA(t)とおきます。Pは確率であることを示す記号、tはt時間目であることを、AはこのサイトがAであることを示します。このPA(t)を直接αとtで示すにはどうすれば良いでしょうか？ こういう確率と時間の経過の関係を考えるときは、1時間たった後に確率がどう変化するかを考えるのが常道です。そこで、t+1時間後にこのサイトがAである確率（これは、PA(t+1)という記号で表記できます）を考えてみます。t+1時間後にこのサイトがAであるということには、次の２つの場合が考えられますよね。

2a.  t時間目にはこのサイトがAであった。t+1時間後にも変化していない
2b.  t時間目にはこのサイトはA以外であった。t+1時間後に変化してAになった

３．上のそれぞれを文章をよくみると、前半（t時間目におけるサイトがどのようなものであるか）と後半（1時間経過してサイトに変化があるかどうか）の２つの確率が含まれています。
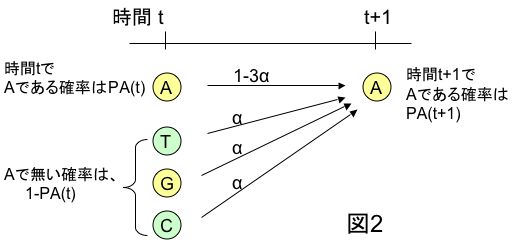
まず、前半ですが、t時間目のサイトの状態を、PA(t)という記号を用いて、次のように表せます。〔図２のt時間のところ〕

3a.  t時間目にこのサイトはAだった。その確率はさっき仮定したように、PA(t)
3b.  t時間目にこのサイトはA以外だった。その確率は、上の場合では無いということですから１から引けばよく、1-PA(t)

４．次に、 2a, 2bの後半の文章にある「変化していない」、「変化してAになった」に注目してみましょう。t時間目にサイトが「変化していない」というのは上の1の説明にあったように、1-3αで示されます。また、t時間目にはAで無かったものが「変化してAになる」確率はαですよね。〔図２の矢印のところ〕

4a.  t時間目とt+1時間後ではサイトは変化していない。この確率は　1-3α
4b.  t時間目とt+1時間後ではサイトは変化してAになった。この確率は　α

５．これでt+1時間目に問題のサイトがAであるときの２つの場合(2a, 2b)の説明は終わりです。図2に概念図を示しておきました。２つの確率（3aと4a、3bと4b）をそれぞれかけ合わせると、 2a, 2bそれぞれの場合の確率が出ます。

2a.  t時間目にはこのサイトがAであった。t+1時間後にも変化していない。　この場合の確率は(1-3α) x PA(t)
2b.  t時間目にはこのサイトはA以外であった。t+1時間後に変化してAになった。　この場合の確率は α x (1-PA(t))

６．いよいよ大詰めです。t+1時間後にこのサイトがAである確率 PA(t+1) は、上の2a, 2bのそれぞれの場合の確率を足し合わせたものですから、

PA(t+1) = (1-3α)PA(t) + α(1-PA(t))
　　　　= PA(t) - 4αPA(t) + α

です。ここで、t時間目からt+1時間目への１時間に確率がどのように変化するかを考えて見ましょう。それぞれの時間における確率を単純に引き算して PA(t+1) - PA(t) を計算すれば良いのですが、上の計算式を変形すれば、PA(t+1) - PA(t) を左辺にもって来られます。

PA(t+1) - PA(t) = -4αPA(t) + α

１時間が経過する時のP(A)の変化を、一定時間の変化を表す記号ΔPA(t)を用いて表現すると、

ΔPA(t) = PA(t+1) - PA(t) = -4αPA(t) + α

７．ΔPA(t)で表した形を微分の形で表すと、

dPA(t)/dt = -4αPA(t) + α

とかけます。 これは定数係数1階線形微分方程式の形です（興味のある人は自分で勉強して下さい）。 微分方程式の公式に従って、PA(t)の解をもとめると、

PA(t) = 1/4 + (PA(0) - 1/4) e ^ (-4αt)

ここで PA(0)というのは一番最初の前提で、問題のサイトがAであるということなので、PA(0) = 1です。 そのため、

PA(t) = 1/4 + (PA(0) - 1/4) e ^ (-4αt)
	= 1/4 + (1 - 1/4)  e ^ (-4αt)
	= 1/4 + 3/4  e ^ (-4αt)

逆に、問題のサイトがAで無ければ、PA(0)=0なので、

PA(t) = 1/4 - 1/4  e ^ (-4αt)

これで、t時間目に問題のサイトがAである確率が出ました。

８. 上の微分方程式のところはともかくとして、t時間目に問題のサイトがAである確率が出たのですから、内容をもうすこし拡張してみます。もう微分とかの難しい式はでてこないので、安心して下さい。まず、先ほどまでと確率の書き方を変えて、問題のサイトが最初Aでt時間後にもAである確率をPAA(t)で表し、同様に、最初Gでt時間後にAである確率をPGA(t)で表すと、

 PGA(t) = 1/4 - 1/4  e ^ (-4αt)
 PAA(t) = 1/4 + 3/4  e ^ (-4αt)

と書くことができます。今のモデルでは塩基置換が起こる確率は全て等しいため、最初の塩基がCでもTでも同じ確率でAになりますから、PGA(t)=PCA(t)=PTA(t)です。つまり、上の式は、初期状態の塩基 i （iはATGCのいずれか）がt時間後に同じ塩基 i のままであるか、異なる塩基 j に置換されているかという２つに分けられます。このことを上にならってPii(t), Pij(t)で表すと、

Pii(t) = 1/4 + 3/4  e ^ (-4αt)
Pij(t) = 1/4 - 1/4  e ^ (-4αt)
但し、i ≠ j

となります。これで、ある時間tにおける問題のサイトが初期状態から変化したときと、変化しなかったときの確率を一般化できました。

９. さて、上の説明でαは、ある塩基が別の塩基に単位時間当たりに（上の説明では話を簡単にするために１時間にした）変化する確率でした。それでは、このモデルを用いて、時間あたりサイトあたりの塩基置換率（λ）を考えてみましょう。塩基置換というのは、あるサイトのある塩基が他の３つの塩基のどれかに変化することです。それぞれの塩基に変化する確率は、このモデルではαですよね。では、サイトあたりの変化の確率である塩基置換率は、ある塩基が他の３つのうちのどれかに変化する確率ですから、３通りの確率を加えたものということで、λ = α+α+α = 3α になります。このλをつかって8の式を書き換えると、

Pii(t) = 1/4 + 3/4 e^(-4λt/3)
Pij(t) = 1/4 - 1/4 e^(-4λt/3)

になります。

回答は下の回答欄をメールの本文にコピーして（＊添付書類にはしないで下さい）、１〜９までの項目のうち理解できたもの、理解できなかったものの番号を記入して、梶田宛にメールで送って下さい。7月5日までに提出して下さい。
＜ここから＞
回答欄
理解できた項目：
理解できなかった項目：
コメント：
＜ここまでコピー＞