![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
Rを使ったデータ解析 †第9回授業の獲得目標:
|
| 演算子 | 意味 | 使用例 |
| + | 足し算 | > 4+3 [1] 7 |
| - | 引き算 | > 4-3 [1] 1 |
| * | 掛け算 | > 4*3 [1] 12 |
| / | 割り算 | > 4/3 [1] 1.333333 |
| ^ | 累乗 | > 4^3 [1] 64 |
| %/% | 整数商 | > 7%/%3 [1] 2 |
| %% | 剰余 | > 7%%3 [1] 1 |
Rでは、好きな名前をつけたオブジェクト("もの")に、数値や文字列などのデータを代入できます。オブジェクトには大文字小文字の区別があります。
> x = 3 #xに3という数字を代入した > X = 4 #Xに4という数字を代入した > x + X #xとXの足し算 (なお、#の後はコメント文と呼ばれ、処理には関係の無い説明を書いておける)
なお、上では"="を使って数値を代入しましたが、 "<-"を使っても同じことができます。
> x <- 3 > X <- 4 > x+X
(Rの代入はもともと "<- " だけだったが、比較的最近、 " = " も使えるようになった)
![[smile]](image/face/smile.png) †
†みなさんは、沢山のデータを1まとめにして扱う方法をすでに知っている。 例えばエクセルを使った計算では、
| 10.4 | 5.6 | 3.1 | 6.4 | 21.7 |
という表を使ってデータを一まとめにし、sum()関数をつかったり、1つのセルに5を足すという計算結果を全部のセルにコピペして、全ての値に5ずつ0足した結果を得たりした。
でも、Rのように、命令文を1行ずつ入力して計算するソフトウェアの場合、データをまとめて扱うにはどうすればいいだろうか?
もちろん、下のように1行ずつ計算式を打ち込んでも答えはでるが、データの数が多くなると、面倒すぎる。
(こんなやり方だと面倒くさい) > 10.4+5.6+3.1+6.4+21.7 > 10.4+5 > 5.6+5
そこで、Rでは、たくさんのデータを一まとめにして扱うときには、カンマで区切って横1行に並べて使う。このようなデータの構造をベクトルと呼ぶ。ベクトルとうと、高校の数学でやった「大きさと方向をもった量」を思い出すと思うが、
Rで使うベクトルは、同じ種類のデータに順番をつけて並べたもの
と定義しておこう。これは、Rが沢山のデータをまとめて処理するために用いる、データの構造だ。例えば、
(10.4, 5.6, 3.1, 6.4, 21.7)
というデータの集まりは、同じタイプのデータに順番をつけてひとまとめにしたものであり、Rでいうところのベクトルだ。
そして、Rでデータを一まとめにして使うときに必要なのが、c()という関数。
| Rを使う上で、これだけは絶対に覚えておこう |
| Rでデータを一まとめにして扱うときには、 c() という関数を使う |
例えば、上のデータを、x というオブジェクトに代入したいときには、
x=c(10.4, 5.6, 3.1, 6.4, 21.7)
という命令を使う。上の命令を入力した後、「 x 」とだけ入力すると、xの内容が表示される。
> x [1] 10.4 5.6 3.1 6.4 21.7
上の結果に表示された[1]は何だろうか?これは、表示された行の最初の数字が、ベクトルの1番目の要素だということを意味している。では、次のようなベクトルをyに代入して、内容を表示させてみよう。
> y=c(1984,1985,1986,1987,1988,1989,1990,1991,1992,1993, 1994,1995,1996,1997,1998,1999,2000,2001)
ウィンドウの大きさによって表示のされ方は異なるが、もし1行に収まらなければ、
> y [1] 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 [15] 1998 1999 2000 2001
というように、2行目の始まりに[15]というような数字が表示される。これは、2行目が15番目の要素から始まっていることを示している。
「ベクトル」とは、同じタイプのデータに順番をつけて一まとめにしたものだった。では、一まとめの中から、例えば、「5番目の要素」だけを取り出すにはどうすればいいだろうか?勘のいい人はもう気づいているかもしれないが、
> y[5] [1] 1988
と、オブジェクトの名前に順番を[]に入れたものをくっつける事で、目的の要素を取り出すことができる。
では、Rで、沢山のデータを一まとめにして、いろいろ計算してみよう。
まずはおさらい。上で出てきた、 c() という関数を使って、オブジェクトにデータを代入でする。
> x=c(1,2,3,4,5,6,7) >
entterキーを押しても何もおこらない?いえいえ。エラーメッセージが何も表示されず、新しいプロンプトが表示されたら大成功。
(もし、上のようにならなかった人は、半角・全角の文字の違いとコンマやカッコに注意してもう一度やってみよう。)
では、プロンプトの後に"x"と入力して、結果を見てみよう。
>x [1] 1 2 3 4 5 6 7
上の様に表示されれば「xというオブジェクトに(1,2,3,4,5,6,7)が代入されたことになる。では、このデータを対象に、統計解析の基本である平均値の計算を計算してみよう。
mean()という関数(meanは英語で平均値の意味)で一まとめにしたデータ(ベクトル)の平均値が計算できる。 命令の入力に自信の無い人は、下の囲みの中をコピー・ペースト。 >mean(x) [1] 4
平均値"4"が表示されれば大成功(これで、あなたがRを使って行う、初めての統計解析は、無事に成功した)
では、数値をもう少し変えて、自分の好きな値で計算してみよう。。。
上で説明したように、キーボードの"↑"記号を何回か押してみると、
> x=c(1,2,3,4,5,6,7)
と表示された。そしたら"←"と"Back space"などを使って、数値を好きに変更して、最後に"Enter"キーを押そう。
> x=c(1232,223.33,3 ,4 , 5666)
半角文字であるかぎり、別にスペースがいくつ入っていても大丈夫。入力したら、上と同じことをしてみると、
> x [1] 1232.00 223.33 3.00 4.00 5666.00 > mean(x) [1] 1425.666
これで、自分の好きな値を入力して、平均を計算することができた。
![[smile]](image/face/smile.png) †
†生物学を学ぶ限り、自分が実験や観察で得たデータを使うときに、統計解析は必ず使うことになる。生物学のための統計解析の本も、数多く出版されている。一年生の皆さんも、機会をみつけて、できるだけ統計学に慣れ親しんでおいて欲しい。そんなとき、Rは非常に役に立つ。Rは非常に強力な統計解析ソフトであるため、与えられたデータの持つ統計的特徴を瞬時に計算したり、データの持つ意味を推測するための図版を一瞬に作図してくれる。この授業ではRを使って実際にデータを解析することで、統計解析に慣れ親しむ方法を解説する。実際の理論的裏付けは、統計の本を読んだり、授業に出たりして、各自学習してほしい。
この授業では統計解析を、次の2つの目的のために使う。
1. ある対象(母集団)から得られた部分的な数値データから、その対象の持っている性質や特徴を知ること
2. ある対象や実験で得られた数値データを用いて、その対象についてどういう判断を下せば良いかを論じること
"ある対象(集団)から得られた部分的な数値データから、その対象の持っている性質や特徴を知ること"
っていうけれど、「母集団」って何?
「母集団」というのは、興味の対象になっている集団全体のことだ。~例えば、
生物学の大きな目的の一つに、自然界に存在する様々な生物の特徴を知ることがある。しかし、自然界の全ての生物個体を計測して、特徴を知ることは不可能。そこで、対象とする生物から、一部だけ(標本)を偏り無く取り出して(これを任意抽出とかランダムサンプリングと呼ぶ)、特徴を計測し、対象生物全体(母集団)の特徴を推定する。こういう作業を「統計的推測」と言う。
この、「一部を使って全体を知る」という点が、が統計の基本だろう。
生態学などのマクロ系の生物学では、上のような方法で標本を採集し、母集団の性質の解析に統計学的手法を用いることが、非常に多くある。この授業では、統計学全般について語っている時間は無いので、ほんのさわりしか扱わないが、下に示す参考書などを読んで、勉強しておいて欲しい。受験で培った数学力が落ちておらず、学問に対する情熱が非常に高い、1年生の今が統計学習得のチャンスですぞ!
それでは、実際に統計的推測やってみよう。。
【ここをクリック】←ここに、産業技術総合研究所 デジタルヒューマン研究センターから提供して頂いた、1997年の男子大学生110人の身長、体重のデータがある。このデータを使って、1997年当時の大学生の身長と体重の一般的傾向について議論してみよう。
このとき、
母集団は1997年当時の大学生全て
標本は1997年の男子大学生110人
今回の統計的推測では、
110人分のデータから、1997年当時の大学生全体の身長と体重の傾向を推測する
ことを目的としている。
| データを一まとめにしてオブジェクトに代入する2番目の方法 |
| コピー・ペーストや手入力でデータをまとめたいときには、scan() という関数を使う |
> h=scan() 1:
画面に表示された 1: の後に、上のページから身長データをコピー・ペーストして、最後にenter キーを押す。次のように表示される。
1: 1775 1710 .. ..<省略>.. 111:
同様にして、体重データも w というオブジェクトにを入れる。次のように表示される。
1: 79.8 58.0 .. ..<省略>.. 111:
確認のために
> h > w
と入力。データが一覧表示される。
計測データが得られたら、まずは、グラフにしてみるよう。グラフとして視覚化することで、データの持つ性質が直観的に理解できる。こういうとき、Rは、いろんなグラフを一瞬にして描画してくれるので、非常に便利。
まずはヒストグラム(柱状グラフ)を使っみる。Rを使ってヒストグラムを書く場合は
> hist(h)キーボードからたった7文字打ち込むだけで、身長の度数分布がグラフで表示される。
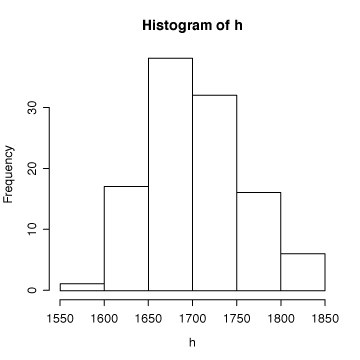
このグラフを見ただけで、標本データでは身長170cmぐらいの学生が最も多く、 データは釣り鐘型の分布をしている。ということが分かる。同様のことを体重についてもやってみよう。
> hist(w)
次に、この標本データの平均とか最大値とか、最小値とか、データの集まりがもっている基本的な性質を表示させて見よう。次のように入力。
> summary(h) Min. 1st Qu. Median Mean 3rd Qu. Max. 1578 1671 1700 1706 1734 1839これで、1997年当時の調査した大学生110人の身長は、平均170.0cm(最大:183.9cm, 最小: 157.8cm)ということが分かった。1st Qu.と3rd Qu.というのは、全体の4分の1の人数がどの高さまでの間に含まれているかということを表している。つまり、167.1cm以下の人が25%、173.4cm以上の人が25%、その間の人が全体の50%ということ。
> summary(w)
身長も体重も釣り鐘型の分布になっていた。では、この2つの数値の間に何か、関係があるだろうか?これもまた、グラフで表示させてみる。こういう場合、縦軸に体重、横軸に身長をとって、一人一人の持つ身長と体重の散布図を作る。Rの場合、次のように入力するだけ。
> plot(h,w)身長と体重の関係は右上がりの直線関係にありそうだ。
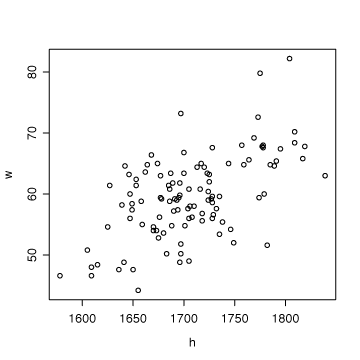
今回、110人分のデータを使って、1997年当時の大学生男子の身長と体重について、
グラフによる視覚化 要約統計量の表示 散布図の作成という3つのことを行った。この標本が母集団の性質を表しているとするならば、1997年当時の大学生について、次のような推定ができる。
1997年当時の男子大学生は、身長の平均が170.6cmで、データは釣り鐘型に分布している 体重は平均が59.53kgで、身長と同様にデータは釣り鐘型に分布している 身長と体重の間には、正の相関があるこれで、1997年当時の男子大学生という母集団の身長・体重について、統計的推定を行うことができた!
なお、今回は分散や標準偏差の話しは省略した。Rを使った統計解析の基本(データの図示、代表値の計算、データ間の相関)などについてはここでは説明しきれないので、下のリンクにある中澤さんによる解説などを読んで、勉強してみて欲しい。。
![[smile]](image/face/smile.png) †
†この授業で対象とする統計解析の2つめは、
"ある対象や実験で得られた数値データを用いて、その対象についてどういう判断を下せば良いかを論じること"
前回の予習課題では、つぎのような設問について考えて貰った。
この設問についてのみなさんの答えは、課題結果のページにまとめてあるが、「A君の方がB君よりもじゃんけんに強いとは言えない」という答えが圧倒的に多かった。
答えてもらったのはいずれも間違いとは言えないので、期限通りに提出した全員が満点となっている。では、ここで、上の設問を、統計的な手法を使って考えてみよう。
後で長い説明があるので、まずは正確さは二の次にして、仮説検定の流れを直観的に理解してもらえるような説明をしてみる。この説明のどこが、後で出てくる「帰無仮説」、「有意水準」、「帰無仮説の棄却」にあたるのかは、後で考えてみて欲しい。なんとなく理解できたら、どれでもいいから統計の教科書を読んでみて、正確に理解することをオススメする。
A君とB君が20回ジャンケンをしたら、B君は5回しか勝てなかった。ジャンケンの勝ち負けって、半々の確率で決まるはずだけど、こんなに勝ち負けが偏ることってあるのかなー?もしかして、A君がズルをしているとか。。
もし、ズルとかじゃなくて、ジャンケンの勝ち負けが、本当に半々の確率で決まっているのなら、...
「20回中5回しか勝てない」っのも、偶然に生じたことなんだろーね。こんなことってよくあるのかなー?
でも、よくあることって、どういう基準で決めればいいんだろう?例えば、数字で表したら、どうなる?
95パーセントぐらいの確率でおこるようなことな「よくあること」って言うことにしようかな(逆に、残りの5%しか起こらないことなら、「滅多に起こらない」ってことだね).
「ジャンケンの勝敗が完全に半々の確率で決まるとして、20回ジャンケンをする実験」を何度も何度も繰り返して、B君がどの程度勝つかをグラフで表してみると...
なんと!!「よくあること」の範囲と考えた全体の95パーセントって、20回中勝つ回数が6回から14回までの場合だっ!
勝つ回数が5回の場合は、残りの5%の範囲に含まれちゃってる...。5%の範囲というのは、「滅多に起こらない」っていうことにした範囲だよなー。
「20回ジャンケンをして5回しか勝てない」っていうのが、「ジャンケンんの勝敗は完全に半々の確率で決まる」という前提の下では「よくあること」では無いというわけだから、「ジャンケンんは完全に半々の確率で決まる」っていうr前提が間違っていたと考える方がいいんだろうね。
うん、きっと、どんな方法かは分からないけれど、A君はB君にジャンケンで勝てる方法を見つけてるんだ
でも、待てよ。「滅多に起こらないこと」の判断基準が5%って大きすぎない?
5%っていうと、、、100回中5回。。。 20回中に1回だ!
っていうことは、もしも、「ジャンケンんは完全に半々の確率で決まる」にしても、20回に1回は、間違った判断を下してしまう可能性があるってことだね。
上の例では、20回のジャンケンの結果を使って統計的検定の直観的な説明を試みた。こんな単純な例であっても、実際の生物学の研究で使う、統計的検定と、推論の進め方は同じだ。(注意: 下の例は、今回のジャンケンの例にあわせるために、かなり説明を端折っている。ここで直観的に理解したら、上記統計の教科書を見てみよう)
まず、統計的検定で、知りたいのは、
「A君とB君が20回ジャンケンをしたとき、5回しか勝てない」という状況は、 「ジャンケンの勝ち負けが、本当に半々の確率で決まる」という前提のもとで、 単なる偶然で起こるようなことか、 あるいは、偶然では滅多に起こらないことか」
ということ。
このように、得られたデータが単なる偶然で生じることかどうかを知るときに、統計的検定という作業が必要になる。
統計的検定では、次のような論証う。
A君とB君のジャンケンの勝敗は、半々の確率で決まるこの仮説のことを 帰無仮説と言いう。(統計の教科書を見ると、帰無仮説には「違いがない」とか「差がない」という仮説を使うと書かれている。今回の場合「『ジャンケンの勝敗は、半々の確率で決まる』というだけで、『差が無い』とか『違いが無い』とかは言って無いじゃないか?」と思う人がいるかもしれない。しかし、「ジャンケンの勝敗は、半々の確率で決まる」ということは、「ジャンケンの勝ち・負けそれぞれが生じる確率には違いが無い」ということを意味している。字面だけで判断するとこんがらがる場合があるので、要注意。)
A君とB君のジャンケンの勝敗は、半々の確率ではきまらない(A君はB君よりもジャンケンに強い)というもの。対立仮説は帰無仮説を否定したものになっている。
p値の計算をするときに、「20回中勝ちが5回」の場合だけを計算するだけではなく 20回中勝ちが5回以下(5, 4, 3, 2, 1, 0)の場合の確率も計算しなくてはならないということということ。この後の議論に出てくるように、起きた事象がどれだけ希にしか起きないことかを判断して、それが滅多におこらないようなことなら、前提となった帰無仮説が間違っていると判断する。つまり、「勝ちが5回以下」のそれぞれのできごとは「勝ちが5回」という出来事よりも起こりにくいことなので、そう言う場合にも、帰無仮説は棄却される。そのため、p値の計算は「5回以下」の場合の確率が必要になるの。この確率のことを累積確率と呼ぶ。
hist(xlim=c(0,20),rbinom(10000,20,0.5)) で表示させた
今回の解説では、片側検定、両側検定の話しは意図的に省略してある
「A君とB君のジャンケンの勝敗は半々の確率で決まる」(帰無仮説)
(この場合、5回しか勝てないというデータの偏りは単なる偶然)
が棄却されたので、
「A君とB君のジャンケンの勝敗は、半々の確率ではきまらない」
(対立仮説)(この場合、データの偏りは、単なる偶然では無い)
「A君とB君のジャンケンの勝敗は、半々の確率で決まる」(帰無仮説)が正しいという仮定の下で、「20回中5回しか勝てない」という状況が生じる確率(p値)が、「希なことなのか、そうでないのか」の判断基準(有意水準)よりも大きい。言い換えると、「A君とB君のジャンケンの勝敗は、半々の確率で決まるときに、20回中5回しか勝てないという状況は、別に不思議ではない」ということ。つまり
「A君とB君のジャンケンの勝敗は、半々の確率で決まる」(帰無仮説)という仮説は 棄却 されない得られたデータからは帰無仮説を否定できなかったので、この場合、得られたデータ(この場合、ジャンケン20回におけるA君B君の勝率い)には...%の有意水準で、有意差が無いと言う。ここで注意しなければならないのは、「有意差が無い」からといって、「A君とB君のジャンケンの勝敗は、半々の確率で決まる」と結論づけてはいけないこと。「有意産が無い」のは、「A君とB君のジャンケンの勝敗は、半々の確率で決まっていてもおかしくはない」ということを意味しているだけで、単なる偶然の結果かもしれないし、データ数が少ないせいかもしれないし、いろんな場合があり得る。
では、実際に先ほどの例をRを使って解析してみよう。この検定は二項検定と呼ばれている。また、ここでは有意水準を5%としよう。
まず、帰無仮説は
A君とB君のジャンケンの勝敗は、半々の確率で決まる
ということ。この帰無仮説が正しいと仮定すると、 得られたデータの偏りは、サンプリングの際の偶然の偏りであると考えられる。ジャンケンの勝ちという、確率50%で生じる事象が、20回中5回得られたわけだが、検定の際には、これより希な条件も全て含めて確率を計算する。つまり、20回中、5回以下と、さらには勝ちの数が15以上の事象が生じる確率を計算。 手で計算してもいいが、今回はすぐにRを使ってみよう。上の検定を行うにはbinom.test()関数を使う。
> binom.test(x,n)
と入力するだけで、実際のx個のサンプルの中で、データ値がn回実現したという状況で、そのデータ値は(もう一つの対になるデータ値に対して)母集団中で1:1で出現するという帰無仮説をテストできる。
このテストの詳しい解説は、上記、粕谷さんの統計の本に載っている。
&ref(): File not found: "Untitled-2.gif" at page "授業/H20/情報処理/09";
上の例だと、20回中5回が勝ちで、帰無仮説は「A君とB君のジャンケンの勝敗は、半々の確率で決まる」だったので、
> binom.test(5,20)
Exact binomial test
data: 5 and 20
number of successes = 5, number of trials = 20, p-value = 0.04139
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.5089541 0.9134285
sample estimates:
probability of success
0.25
p値の値は0.04139なので、有意水準が5%よりも小さい。そこで、帰無仮説「A君とB君のジャンケンの勝敗は、半々の確率で決まる」は棄却される。(もちろん、有意水準を0.001にすると棄却されない)
つまり、「A君とB君のジャンケンの勝敗は、有意水準5%で、半々の確率で決まるとは言えない」ということができる(有意水準0.1%の場合は、「2人の勝率に差があるかどうかはわからない」)。「有意水準5%では、A君とB君のジャンケンの勝敗は、半々の確率で決まるという帰無仮説は棄却された」という言い方もある。
どうやら、やっぱりA君の方がB君よりも強いようだ。もしかすると、B君の癖をよんでいるのかもしれない。
今回の解説では、片側検定、両側検定の話しは意図的に省略してある
先ほど1997年の男子大学生110の身長データをhというオブジェクトに入れた。【ここをクリック】のもう少し下の方には、1998年当時60歳以上の男性51人の身長のデータものっている。大学生(平均20.52歳)と60以上(平均68.61歳)では、48歳ほどの差がある。同じ成人男性といったって、40年も違う時代に成長期を迎えたわけだから、身長には違いがあってもおかしく無いような気がする。この2つのデータをみて、2つのサンプルの母集団(ランダムサンプリングが行われたとして、1997年当時の男子大学生全てと1998年当時の60歳以上の男性全て)の間で身長には差があると言っても良いだろうか?
60歳以上の男性の身長データをオブジェクトに格納。scan()関数を使って
> h2=scan() 1: 1547 1689 .. ..<省略>.. 52:
hとh2のそれぞれの平均値やヒストグラムを比べる。
> summary(h) > summary(h2) > hist(h) > hist(h2)
平均値やヒストグラムを見た限りでは、けっこう違いがありそう。
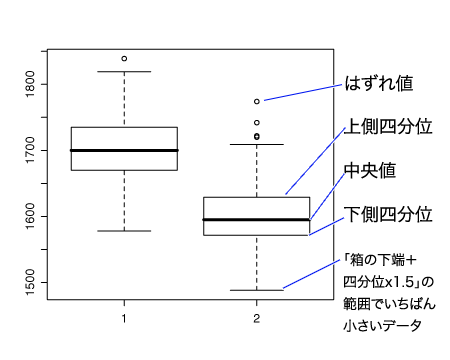
もう一つグラフを作ってみよう。2集団のデータを簡単に比較するときに便利な関数が、boxplot()。
> boxplot(h,h2)
さて、いよいいよ検定。考え方は上で示したのと全く同じ。ただし、データの持っている性質が違うので、p値の計算方法は異なる。このような2集団の違いの検定には、Wilcoxonの順位和検定という方法を使う。検定の説明はブラックボックスになりがちだが、上で紹介した粕谷さんの本や、中澤さんのRの使い方pdfには、詳しい考え方の説明があるので、読んでおいて欲しい。今回はRを使った統計的検定がいかに楽かということを示すのが目的なので、詳しくは触れない。
まず、ジャンケンの例で見たように、帰無仮説と対立仮説を決める。
帰無仮説: 2つのサンプルの母集団の身長に差は無い 対立仮説: 2つのサンプルの母集団の身長に差はある
2つの母集団に違いがなければ、hとh2という集団のデータは、母集団から抽出したときに、たまたま偶然で偏ってしまったものということ。そういう偶然の偏りでこれだけの違いが生じるのは、どのくらいの確率(p値)で生じるのかを計算する。Rではwilcox.test()という関数を使います。
> wilcox.test(h,h2) Wilcoxon rank sum test with continuity correction data: h and h2 W = 4957, p-value = 5.329e-15 alternative hypothesis: true mu is not equal to 0
p値の値は 5.329e-15 で、これは 5.329x10^(-15) を示している。つまり、0.0000000000000005329。これは有意水準の0.01%よりもずーっと小さい値なので、2つの身長データの違いが同一母集団から偶然のサンプリングのバラツキでで生まれたということはほとんど無い、ということを示している。統計学っぽく表現すると、「2集団の差をWilcoxonテストで検定した結果、0.01%の有意水準で有意な差があった」と書く。
どうやら、40年も年齢の異なる2つの母集団の身長には差があると言って良さそう。やっぱり、成長期に摂取できた栄養の影響などが、きっと大きいのだろう。
./09
*第9回授業・基本課題 **氏名: **課題への回答 -今日の授業の進み方は?(はやい、丁度いい、おそい) --回答: -今日の授業の難しさはどう感じましたか(簡単 丁度いい 難しい): --回答: -難しいと答えた人は、特にどの点が難しかったですか?: --回答: -今日の授業は(分かった 半分ぐらいは分かった 分からなかった): --回答: -分からないと答えた人は、特にどの点が分からなかったですか?: --回答: -今日の講義で分からなかった用語があったら挙げてください: --回答: -授業に関する要望・質問があったらなんでもどうぞ: --回答: ***課題2.Rを使った統計解析:ヒストグラムの表示 &ref(./添付したヒストグラムの画像ファイル名); ***課題3. &ref(./添付したヒストグラムの画像ファイル名); ***発展課題 -問1の答え:身長の平均: 体重の平均: -問2の答え:帰無仮説:「 」 -問3の答え:対立仮説:「 」 -問4:検定に用いたRの計算式と結果 計算式: 結果: -問5:検定の結果から議論できること:
手順